trojkaty aska: na okregu o promieniu 3 opisano trojkat rownoramienny o kacie przy wierzcholu rownym 120 stopni. Oblicz dlugosc bokow tego trojkata. prosze o pomoc

AROB: pomagam

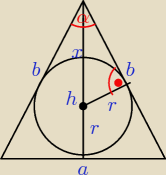
AROB: Dane: r = 3, α=120⁰ −−−−−−−−−−−−−−−−−−− a, b = ?

r		α
	= sin		x = h − r
x		2

3
	= sin600
h−r

3		√3		6
	=		⇒ h−3 =
h−3		2		√3

	6√3
h−3 =
	3

	6√3		6√3 + 9
h =		+ 3 =		= 2√3 + 3
	3		3

	h		α
Obliczamy b:		= cos
	b		2

	2√3 + 3
		= cos600
	b

	2√3 + 3		1
		=		⇒ b = 4√3 + 6
	b		2

	a   2		α
Obliczamy a:		= sin
	b		2

	a		√3
		= b * sin600 ⇒ a = 2b *		= b√3 =
	2		2

= (4√3 + 6) * √3 = 12 + 6√3 a = 6(2 + √3)

Eta: Podam jeszcze inny sposób Δprostokątny ma kąty ostre 60^o i 30^o

	b√3
więc : b = 2h to: a2=
	2

więc a = b√3

	3
IOCI =		...to: IOCI= 2√3
	sin60o

h= IOCI +r => h= 2√3 +3 więc: b = 2*h = 2(2√3+3) [ j ] to a= b*√3 = 2√3(2√3+3) = 6(√3+2) [ j ] wynik ten sam oczywiście Miłych snów, pora Dobranoc

AROB:

Eta: następny sposób

	a +2b
P=p*r , p=		= a2 +b
	2

	b2√3
P=
	4

	a2
i		= sin60o ... to a = b√3
	b

	b2√3		b√3
więc:		=		+b
	4		2

zatem: b²√3= 2b√3 +4b /:b , bo b≠0 to b*√3= 2√3 +4 to b = 2(3 +2√3) więc a = 2√3( 3+2√3) = 6(2+√3) Może być? ..... AROB , Bogdanie Teraz już naprawdę idę spać . Dobrej nocy