? Patryk: https://matematykaszkolna.pl/strona/2261.html tam napisałem na dole rozwiązanie ,gdzie jest błąd

Patryk: ?

Mila: Patryk , gdzie to Twoje rozwiązanie?

Patryk: dokładnie w tym linku https://matematykaszkolna.pl/forum/forum.py?komentarzdo=2261

Patryk: i jak jest ?

Mila: Inna postać:

1		1		sin2x+cos2x
	=		*		=
2cos2x		2		cos2x

	1		sin2x		1		1		1
=		*(		+1)=		(tg2x+1)=		tg2x+
	2		cos2x		2		2		2

Całki różnią się stałą.

Mila: Po obliczeniu pochodnej masz funkcję podcałkową http://www.wolframalpha.com/input/?i=%281%2F%282cos%5E2x%29%29%27

Patryk: czyli mój sposób jest poprawny ?

Patryk: sprawdzenie też zrobiłem i się zgadzało

Patryk: ale to dziwne ,ze mój wynik jest ok Jakuba ok ale one się różnią

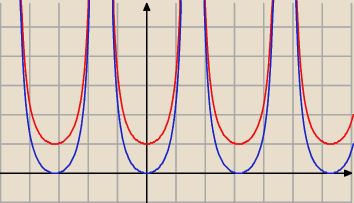
Trivial: Te wyniki się nie różnią − przedstawiają tę samą rodzinę funkcji. Cały sekret leży w stałej całkowania, którą zapewne piszesz mechaniczne i bez zastanowienia. Jako bonus wykresy funkcji: (1) tg²x (2) 1/cos²x Czy zauważasz czym one się różnia?

Mila: Mogą się różnić stałą. Często tak jest. Jednak jeśli obliczysz pochodną, to otrzymasz w obu przypadkach funkcję podcałkową, bo pochodna ze stałej jest równa zero.

Patryk: już zrozumiałem,tak jak napisała Mila ronią się stałą (co można zinterpretować jako przesuniecie wzdłuż OY), co dla liczenia pochodnej nie ma znaczenia ,dzieki

Trivial: Tak. Konkretnie:

	sin2x		sin2x + cos2x		1
tg2x + 1 =		+ 1 =		=		.
	cos2x		cos2x		cos2x