Planimetria dla [z[bezendu]]
5-latek: Zadanie : Pole kola jest trzy razy wieksze od pola prostokata wpisanego w to kolo.
Oblicz stosunek dlugosci boku krotszego do dlugosci boku dluzszego tego prostokata.
7 sie 20:55
bezendu:
hmm miałem właśnie wstawiać zadania z planimetrii do sprawdzania ale skoro już jest to zadanie
to:
Pole koła P=πr2
Pole prostokąta wpisanego w okrą P=a*2r (r−promień czyli połowa bok b ? )
dalej na razie nie mam pomysłu ?
7 sie 21:07
sorry : r to połowa przekątnej tego prostokąta

7 sie 21:09
Saizou : | | 1 | |
promień okręgu opisanego na prostokącie to połowa przekątnej tego prostokąta, czyli R= |
| d, |
| | 2 | |
d=
√a2+b2
7 sie 21:10
5-latek: Narusuj rysunek i oznacz przez R promien kola i przez a ib dlugosci bokow prostokata i
przecztaj dokladnie 1 linijke zadania i uloz rownanie
7 sie 21:10
bezendu:
a no tak masz racje poła przekątnej

7 sie 21:10
Saizou : 5−latek czy ten wyniki jest taki 'brzydki'

7 sie 21:12
bezendu:
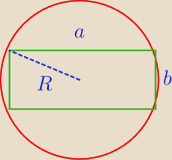
7 sie 21:13
5-latek: Tak bedzie troche brzydki ten wynik Bezendu z warunku zadania masz ze 3a*b=πR2 i skorzystaj z
pitagorasa
7 sie 21:16
bezendu:
P=πR
2
zgadza się ?
7 sie 21:16
Saizou : ale R jest do kwadratu

7 sie 21:18
7 sie 21:19
5-latek: Moze tak a2+b2=4R2 wyznacz z tego R2i wstaw to do rownania 3ab=πr2 i licz dalej
7 sie 21:20
sorry : | | √a2+b20 | |
Można by rzec : 3π |
| = a * b |
| | 2 | |
7 sie 21:21
bezendu:
a z tego co ja zrobiłem ?
7 sie 21:22
sorry : kurde kwadrat

7 sie 21:22
Saizou : ale to
bezendu proponuje też jest dobrze
| | 1 | | 1 | |
Pk=π*R2=π*( |
| √a2+b2)2= |
| π(a2+b2) |
| | 2 | | 4 | |
7 sie 21:22
5-latek: Ja poczekam na wasze rozwiazania

7 sie 21:25
Saizou : a mogę ja też

7 sie 21:26
7 sie 21:27
bezendu: Saizou i co dalej z tym ?
7 sie 21:27
Saizou : przeczytaj jeszcze raz treść xd
7 sie 21:27
bezendu: ale właśnie jak obliczyć ten stosunek ?
7 sie 21:29
Saizou : to zapisz równanie i zobacz co można zrobić xd, równanie z parametrem lub podzielić przez
kwadrat dłuższego boku
7 sie 21:31
7 sie 21:33
sorry : wtf
7 sie 21:33
bezendu:
@sorry doceniam to, że chcesz zrobić to zadanie ale mógłbyś nie pisać w tym poście już ?
ewentalnie dać wskazówki ?
7 sie 21:36
bezendu:
Saizou jak zdefiniować bok krótszy ?
7 sie 21:37
5-latek: bezendu . Ja bym robil dalej tak . Wyznaczam R2 i wstawiam do 1 rownania i otrzymam takie
rownamie πa2−12ab+πb2=0 ale my szukamy stosunku a/b wiec dalej kombinuj. Zobacz co
proponuje Saizou o godz 21.31
7 sie 21:41
Saizou : trzeba to napisać w założeniach np. a<b lub przyjmuję dane jak na rysunku (tylko trzeba pokazać
wyraźnie, który bok jest krótszy)
7 sie 21:45
bezendu: mam wyznaczone R
2 bo już wcześniej podstawiłem
stosunek będzie wygladał tak krótszy bok to a dłuższy to b czyli
7 sie 21:48
Saizou : tak

7 sie 21:49
5-latek: Tak. Tylko popraw u siebie na rysunku bo nie zwracalem na niego wiekszej uwagi .
7 sie 21:49
bezendu:
to jaki kolejny krok ?

7 sie 21:51
Saizou : pomyśl musisz otrzymać coś takiego
| | a | | a | |
π( |
| )2−12 |
| +π=0 b>a>0 |
| | b | | b | |
i jak myślisz co dalej?
7 sie 21:54
sorry : zrobiłem
7 sie 21:57
sorry : πr
2 = 3ab
4r
2=a
2 + b
2
Rozwiąż równanie kwadratowe

7 sie 22:01
5-latek: Dobrze bezendu . To rownanie ktore podal CI saizou ptrzymasz kiedy rownanie πa
2−12ab+πb
2=0
podzielisz stronami przez b
2 . Ale dalej to juz sobie radz sam

7 sie 22:04
7 sie 22:06
sorry : | a | | 9−√81−π2 | | 9+√81−π2 | |
| = |
| v |
| |
| b | | π | | π | |
Co o tym sądzicie ?
7 sie 22:12
Saizou : no raczej nie, bo jeśli liczyłeś ze swojego równania to masz błąd
7 sie 22:12
sorry : gdzie ?
7 sie 22:13
bezendu: popatrzałem na równanie sorry i to mnie zmyliło
7 sie 22:14
5-latek: OK tylko moze zapisz ja tak Δ=144−4π2 i jak ona musi byc i dlaczego
7 sie 22:15
Saizou : jest tylko jeden stosunek jbc

7 sie 22:16
5-latek: | | a | |
Sorry z tresci zdania 1> |
| |
| | b | |
7 sie 22:18
sorry : ale obliczenia są prawidłowe ?
7 sie 22:19
sorry : aaaaaaa
7 sie 22:20
Saizou : Δ=144−4π=4(36−π)
√Δ=2
√36−π
| | 12−2√36−π | | 6−√36−π | |
t1= |
| = |
| |
| | 2π | | π | |
| | 6+√36−π | |
t2= |
| >1 sprzeczność |
| | π | |
7 sie 22:23
5-latek: saizou pod pierwiastkiem ma byc π
2 
7 sie 22:29
Saizou : tak ma być π
2, ale gdzieś go zjadłem xd

7 sie 22:34
5-latek: bezendu . Delta z tego rownania musi byc wieksza od zera bo rownanie musi miec dwa rozne
pierwiastki .−−−jakie?
Jesli rownanie ma dwa rozne pierwiastki to mozesz skorzystac z ewzorow Vietea
| | a | |
dla tego rownania iloczyn pierwiastkow =1 ale wlasnie z tresci zadania mamy ze |
| <1 wiec |
| | b | |
jak policzysz pierwiastki tego rownania to musisz wybrac ten ktory spelnia warunki zadania
7 sie 22:39
7 sie 22:40
bezendu:
czyli to co miałem w poście 22:06 większe od zera ?
7 sie 22:41
5-latek: bezendu latwe bylo zadanie ?
To teraz tez latwe
Dany jest trojkat rownoramienny o podstawie 8i wysokosci 3
W trojkat ten wpisano okrag a nastepnie poprowadzono styczna do okregu rownolegla do podstawy
trojkata oblicz dlugosc promienia okregu oraz dlugosc odcinka stycznej zawartego miedzy
ramionami trojkata .
7 sie 22:44
bezendu: łatwe

z tamtym miałem problem

7 sie 22:46
5-latek: tak bezendu wieksze od zera . A to tylko potrzebne CI to bylo do tego zeby wyliczyc pierwiastki
Nie mogla byc =0 bo wtedy jest jeden pierwiastek podwojny i co bys dostal zamiast prostokata .
Tez <0 bo nie ma rozwiazan.
7 sie 22:50
5-latek: Podstawa to dobrze wykonany rysunek
7 sie 22:51
bezendu: Tak wiem o tym

dziękuje za zadanie

7 sie 22:56
Trochę umiem matematykę : Czyli co ja mam źle?
7 sie 23:01
Saizou : bezendu zadanie jest bardzo proste

7 sie 23:04
bezendu: Saizou może dla Ciebie

7 sie 23:16
Saizou : hehe to zrób rysunek i się przekonasz xd
| | 8 | |
długość stycznej między ramionami |
| |
| | 9 | |
czy jakoś tak
7 sie 23:20
5-latek: Ijeszcze jedno zadanie i starczy.

W trojkacie ABC gdzie bok AC to podstawa trojkata porowadzono dwusieeczna kata wewnwetrznego
ABC ktora przecina bok AC w punkcie D >Dlugosci odcinkow AD i AC sa rowne a i b (a>b) Przez
srodek O odcinka BD prowadzimy prosta prostopadla do BD ktora przecina przedluzenie boku AC
w punkcie X . Oblicz dlugosc odcinka XD.
7 sie 23:24
5-latek: bezendu no to zabieraj sie za nastepne zadanie .
jaki znasz wzor na pole trojkata w zaleznosci od promienia okregu wpisanego w trojkat
8 sie 21:01
bezendu:
| | 1 | |
trójkąt równoboczny r= |
| h o to chodzi ? |
| | 3 | |
8 sie 21:04
5-latek: tak nawiasem mowiac to tam ma byc trojkat rownoramienny
A znazz taki jak Ptr=p*r
jak przeczytasz dobrze tresc to jeszcze napisz drugi wzor na pole trojkata . Zrob porzadny
rysunek
8 sie 21:11
Saizou :
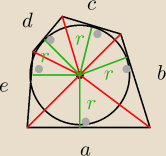
dla dowolnego wielokąta zachodzi (ja pokażę dla 5−kąta)
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
P5−kąta= |
| ar+ |
| br+ |
| cr+ |
| dr+ |
| er= |
| r(a+b+c+d+e) |
| | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
| | 1 | |
oraz p= |
| (a+b+c+d+e), otrzymamy |
| | 2 | |
P
5−kąta=pr
8 sie 21:14
bezendu: nie znam tego wzoru.
8 sie 21:15
bezendu: | | 1 | |
jest taki wzór P= |
| (a+b+c) i zastanawiało mnie to właśnie  |
| | 2 | |
8 sie 21:15
Saizou : P=p*r, gdzie p to połowa obwodu
2P
t=(a+b+c)r
8 sie 21:18
5-latek: Bezendu nie duze P bo to jest symbol pola tylko male p bo to co napisales to jest polowa obwodu
8 sie 21:19
bezendu: ok zapamiętam
8 sie 21:20
Saizou : możesz też zamiast P pisać S , gdzie P=S− pole figury
S=pr , gdzie p− połowa obwodu
8 sie 21:21
5-latek: No to ile = polowa obwodu ?
8 sie 21:24
5-latek: | | 2Ptr | |
Lub z tego wzoru na r = |
| ile rowna sie a+b+c |
| | a+b+c | |
8 sie 21:26
5-latek: Zrob tez rysunek bo bedzie potrzebny do obliczenia dlugosci stycznej
8 sie 21:30
Saizou :
o tyle, wiem że trochę nie kształtnie, ale może być xd
8 sie 21:30
5-latek: Saizou nie z przymiotnikami piszemy razem

8 sie 21:33
Saizou : oj tam, wiem wiem i 'nie piszemy', tylko raczej forma 'pisze się' (forma bezosobowa), bo to
tyczy wszystkich, a nie tylko wąskiej grupy xd
8 sie 21:36
5-latek: 
8 sie 21:38
5-latek: Bezendu . W zadaniu masz dana podstawe i wysokosc . Ile = pole tego trojkata ?
Poza tym do policzenia obwodu skorzystaj z Pitagorasa >
8 sie 21:40
bezendu: połowa podstwy to 4 pi a wysokość 3
(4π)2+32=c2
16π2+9=c2
tak ?
8 sie 21:42
5-latek: Bezendu czy to naprawde jestes Ty? Przeciez podstawa =8 a nie 8 π
8 sie 21:45
bezendu:
32+42=x2
9+16=x2
x2=25
x=5 lub x=−5∉R+
8 sie 21:49
5-latek: Dobrze czyli dlugosc ramienia =5 a to jest trojkat rownoramienny wiec ile wynosi obwod tego
trojkata ?
8 sie 21:51
bezendu: obwód 18 (ja jestem kolorowy )
8 sie 21:52
5-latek: Masz podane w zadaniu ze podstawa =8 a wysokosc =3 wiec ile wynosi pole tego trojkata
8 sie 21:54
Saizou : można też znać japoński i zobaczyć że połowa obwodu to 9

(mój post z 21:30)
8 sie 21:56
5-latek: Dobre to

8 sie 21:58
bezendu: P=12 [j2]
8 sie 21:58
bezendu: saizou wejdź na gadu

8 sie 22:01
5-latek: Masz dane pole trojkata i obwod
wiec teraz ze wzoru P=p*r lub ze wzoru co podal Saizou z godz 21.18 oblicz r .
8 sie 22:02
8 sie 22:05
5-latek: OK . No to teraz bierz sie za obliczenie dlugosci stycznej . ladny rysnek prosze
8 sie 22:07
bezendu: chwilkę
8 sie 22:10
bezendu:
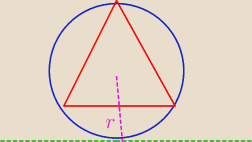
8 sie 22:13
Saizou : bezendu chyba coś nie teges z tym rysunkiem xd
8 sie 22:19
5-latek: W trojkat wpisano okrag a nieodwrotnie
8 sie 22:19
5-latek: POza tym gdzie sa oznaczenia
8 sie 22:21
bezendu: jak robię oznaczenia to mi rysunek się nie ładuję

8 sie 22:24
bezendu:
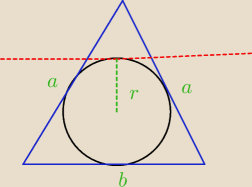
8 sie 22:29
5-latek: To zrob rysunek i przyjmij oznaczenia oznaczenia podstawa trojkata AB dlugosci ramion AC i
BC
wysokosc trojkata CD dlugosc stycznej EF , punkt stycznosci stycznej EF z okregiem oznacz np
przez G
8 sie 22:32
bezendu: opierajmy się na rysunku 22:29
8 sie 22:37
5-latek: To powiedz ja chcesz napisac proporcje do wyliczenia dlugosci stycznej
To chociaz oznacz dlugosc tej stycznej
8 sie 22:44
bezendu: ale jeśli wprowadzam więcej jak 4 litery to rysunek mi się nie ładuje dlatego napisałem że
musimy działać na tym

8 sie 22:45
5-latek: Przeciez to nie powinien byc dla Ciebie zaden problem pisac te oznaczenia ktore podalem
No ale jesli chcesz na tym to i tak musisz dla siebie oznaczyc dlugosc tej stycznej przez np c
Musisz tez oznaczyc wyskosc trojkata aab przez np h i dlugosc odcinka od wierzcholka do punktu
stycznosci okregu ze srtyczna przez np d
Teraz zauwaz ze te otrzymamne trojkaty sa podobne to wobec tego jaka ulozysz proporcje zeby
policzyc c
8 sie 23:02
aki:
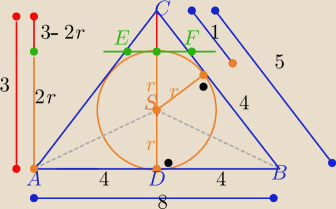
8 sie 23:11
Mila:
Z której godziny zadanie, zrobię rysunek.
8 sie 23:12
5-latek: Bezendu podziekuj ladnie za rysunek wiesz komu

8 sie 23:13
5-latek: Dobry wieczor
Milu jesli mozesz to zrob do zadania z 07.08 z godz 23.24. Bedzie mial na
jutro.

8 sie 23:16
Mila:
Witajcie, wszyscy, chętnie zrobię rysunek, ale długości AD i AC popraw. Może AD i DC?
Pięknie pracujecie.
8 sie 23:26
5-latek: Dobrze
Milu
8 sie 23:29
5-latek: | | EF | | 3−2r | |
Bezendu zobacz . Z rysunku aki  masz |
| = |
| i juz masz wzystko zeby |
| | AB | | CD | |
obliczyc EF wiec policz .
Na jutro do zadania z 07.08 z godz 23.24 zapoaznaj sie z twierdzeniem o dwusiecznej kata
wewnetrznego i zewnetrznego trojkata .
8 sie 23:35
Mila:
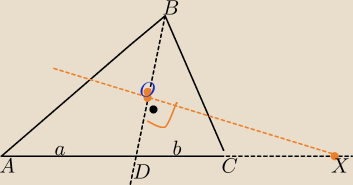
8 sie 23:43
bezendu: Dziękuje za rysunek

Przepraszam ale wczoraj musiałem opuścić forum z przyczyn wyższych

9 sie 11:12
9 sie 11:18
5-latek: A czego dajesz znak zapytania ?
9 sie 16:39
5-latek: Milu bardzo serdecznie dziekuje za rysunek (po remoncie centralnego ogrzewania zabieram
sie za nauke rysowania) a bezendu dorysuje juz sobie sam na Twiom rysunku dwusieczna kata
zenetrznego ABC i oznaczy punkt przeciecia tej dwusiecznej z przedluzeniem boku AC przez Y
9 sie 17:09
Mila:
Załóżcie nowy wątek.
9 sie 21:45
5-latek: Dobrze Milu .

9 sie 21:48
Mila:
Pozdrowienia, jest fantastycznie chłodno, tylko 24o C.
9 sie 21:50
5-latek: Rowniez pozdrawiam

, Wczoraj bylo 35 jak wychodzilem o 15 z pracy wiec dzisiejsze 24
to naprawde chlodno

9 sie 22:04
Garth:
A u mnie dzisiaj dalej 35 bylo.

Poludniowy wschod.
9 sie 22:07
5-latek: Garth . ja mieszkam na Dolnym Slasku i dzisiaj wieczorem lalo i wialo . szkod nie narobilo
tak jak ostatnim razem .
9 sie 23:47















 z tamtym miałem problem
z tamtym miałem problem 
 dziękuje za zadanie
dziękuje za zadanie 


 W trojkacie ABC gdzie bok AC to podstawa trojkata porowadzono dwusieeczna kata wewnwetrznego
ABC ktora przecina bok AC w punkcie D >Dlugosci odcinkow AD i AC sa rowne a i b (a>b) Przez
srodek O odcinka BD prowadzimy prosta prostopadla do BD ktora przecina przedluzenie boku AC
w punkcie X . Oblicz dlugosc odcinka XD.
W trojkacie ABC gdzie bok AC to podstawa trojkata porowadzono dwusieeczna kata wewnwetrznego
ABC ktora przecina bok AC w punkcie D >Dlugosci odcinkow AD i AC sa rowne a i b (a>b) Przez
srodek O odcinka BD prowadzimy prosta prostopadla do BD ktora przecina przedluzenie boku AC
w punkcie X . Oblicz dlugosc odcinka XD.
 dla dowolnego wielokąta zachodzi (ja pokażę dla 5−kąta)
dla dowolnego wielokąta zachodzi (ja pokażę dla 5−kąta)

 o tyle, wiem że trochę nie kształtnie, ale może być xd
o tyle, wiem że trochę nie kształtnie, ale może być xd


 (mój post z 21:30)
(mój post z 21:30)










 masz
masz 
 Przepraszam ale wczoraj musiałem opuścić forum z przyczyn wyższych
Przepraszam ale wczoraj musiałem opuścić forum z przyczyn wyższych 

 , Wczoraj bylo 35 jak wychodzilem o 15 z pracy wiec dzisiejsze 24
to naprawde chlodno
, Wczoraj bylo 35 jak wychodzilem o 15 z pracy wiec dzisiejsze 24
to naprawde chlodno
 Poludniowy wschod.
Poludniowy wschod.