Asymptoty Dzikuniii: Muszę zbadać i wykreślić funkcję f(x)=x−1/2x² Wiem, że do obliczenia asymptoty potrzebuje wyliczyć dziedzinę. Dziedzina: 2x² ≠ 0 Df:x∊(−∞,0)∪(0,∞) << nie wiem czy dobrze zapisane i czy wgl powinienem to tak zapisać. Asymptoty: lim(x−>0−)x−1/2x² wychodzi mi −∞ lim(x−>0+)x−1/2x² wychodzi mi −∞ W tym momencie nie wiem jak mam wyszukać asymptot poziomych i ukośnych oraz pionową.

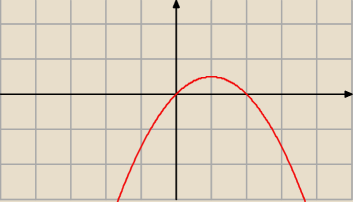
bakałarz: a dyć to zwykła parabola

Dzikuniii: Czyli jeżeli wyszło mi tak jak wyszło (0 dodatnie i ujemne = −∞) to piszę że funkcja nie ma asymptot poziomych, ukośnych i pionowych? Prosiłbym jeszcze o sprawdzenie czy dobrze zapisałem dziedzinę i te asymptoty.

Dzikuniii: up.

Janek191:

	x − 1
y =		; D = R \ {0 }
	2 x2

Dzikuniii: Odświeżam gdyż nie otrzymałem odpowiedzi na moje pytanie.

use: Dziedzine masz dobrze , czy zapiszesz D=R\{0} czy Df; xE(−oo;0)u(0;+oo) to to samo tylko inaczej zapisane.

Dzikuniii: A jak mam wyznaczyć asymptoty poziome i ukośne oraz pionowe (za pomocą obliczeń) jeżeli lim(x−>0−)x−1/2x2 = −∞ lim(x−>0+)x−1/2x2 = −∞

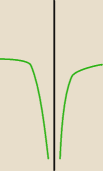
use: Jezeli granice wyszly ci −∞ dla x dążacych do 0 z prawej i z lewej to znaczy to tyle co widac na rysunku wartosci uciekają do −oo czyli asynmptota jest pionowa obustronna x=0. (intuicyjnie sie to przecież wyczuwa zblizasz sie z dziedziną do zera a wartosci uciekają do −oo zera nigdy nie osiągasz a funkcja −oo tez nigdy nie osiąga )

Dzikuniii: Czyli jakbym miał że lim dąży do 0 na − = −∞ i lim dąży do 0 na + = ∞ to wtedy normalnie wyliczam sobie asymptoty poziome, pionowe oraz ukośne ?