proszę w wskazówkę ;)
matura : Dwa samochody wyruszyły jednocześnie naprzeciwko siebie z miejscowości A i B.
Prędkość jednego z nich była o 30km/h większa od prędkości drugiego samochodu.
| | 3 | | 2 | |
W momencie mijania samochody przejechały odpowiednio |
| i |
| |
| | 5 | | 5 | |
odległości między miastami.Oblicz średnie prędkości obu samochodów.
6 sie 20:21
Piotr 10: V+30km/h − prędkość pierwszego samochodu
V − prędkość drugiego samochodu
x− odległość miasta A od B
6 sie 20:26
matura : ale właśnie nie mam podanego czasu ?

6 sie 20:27
Piotr 10: Właśnie czas jest taki sam dla obu samochodów, bo wyruszyli w tym samym czasie
6 sie 20:27
matura : hmm
6 sie 20:29
Piotr 10: | | 2x | |
Wstaw zamiast t w pierwszym równaniu |
| |
| | 5v | |
6 sie 20:29
Piotr 10: I jak idzie?
6 sie 20:32
bezendu:
v+30 dla pierwszego samochodu
v drugi samochód
| 3 | |
| odległość jaką pokonał samochód 1 |
| 5 | |
| 2 | |
| odległość jaką pokonał samochód 2 |
| 5 | |
v=60
v
2=60+30=90
Piotr 10 a bardzo dobrze

6 sie 20:37
Piotr 10: Ale to nie Ty miałeś robić


6 sie 20:38
bezendu: 
6 sie 20:40
Piotr 10: Ale spoko, miejmy nadzieję, że
matura sobie poradził z tym zadaniem już

6 sie 20:42
Bogdan:
| | | | | |
Jest mała nieścisłość w zapisie: |
| = |
| . |
| | v + 30 | | v | |
| | | | | |
Powinno być: s = |AB| i |
| = |
| |
| | v + 30 | | v | |
| | | | | | 5 | |
Można tu nieco uprościć obliczenia: |
| = |
| /* |
| |
| | v + 30 | | v | | s | |
6 sie 20:45
ieska: Pomocy ! Dwa samochody startują z tego samego punktu w tym samym momencie jadą tą samą drogą w
tym samym kierunku do punktu końcowego w tym samym czasie . Pokaż , że w pewnym momencie będą
miały taką samą prędkość
7 sie 16:26
Gustlik:
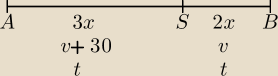
Dwa samochody wyruszyły jednocześnie naprzeciwko siebie z miejscowości A i B.
Prędkość jednego z nich była o 30km/h większa od prędkości drugiego samochodu.
W momencie mijania samochody przejechały odpowiednio 3/5 i 2/5 odległości między
miastami.Oblicz średnie prędkości obu samochodów.
Można bez ułamków, wystarczy trasę podzielić na odcinki 3x zamiast 3/5 i 2x zamiast 2/5:
Oznaczmy:
v − prędkość samochodu B
v+30 − prędkość samochodu A
Ze wzoru s=vt otrzymujemy:
{ 3x = (v+30)t
{ 2x = vt
Dzielimy równania stronami pierwsze przez drugie:
| 3x | | (v+30)t | |
| = |
| i zauważamy, że x i t się skrócą. |
| 2x | | vt | |
| 3 | | (v+30) | |
| = |
| teraz na krzyż jak proporcję: |
| 2 | | v | |
3v=2(v+30)
3v=2v+60
3v−2v=60
v=60 km/h − to prędkość samochodu B
v+30=60+30=90 km/h − to prędkość samochodu A.
8 sie 00:16
bezendu:
Witam
 Gustlik
Gustlik czyli w tego typu zadaniach najpierw zapisujemy stosunek drogi ?
8 sie 00:20
Gustlik: Na równaniach można wykonywać stronami wszystkie cztery podstawowe działania arytmetyczne −
czyli można je dodawać, jak w metodzie przeciwnych współczynników, odejmować, mnożyć i dzielić
jedno przez drugie.
Niestety w szkołach pokazywanie jest jedynie dodawanie stronami, pozostałych metod zaniechano.
Jeżeli masz dwa równania:
{ L
1=P
1
{ L
2=P
2
i podzielisz je stronami, to otrzymasz:
i skracasz, co się da.
Ten sposób jest dobry do równań zawierajacych po obu stronach iloczyny tych samych wielkości,
co pozwala na ich skracanie przy dzieleniu, można więc pozbyć się niewiadomych przez
skracanie.
{ 3x = (v+30)t − to droga przebyta przez samochód A od startu do momentu spotkania,
{ 2x = vt − to droga przebyta przez samochód B od startu do momentu spotkania,
i dzielisz pierwsze równanie przez drugie metodą opisaną powyżej. Wyrugujesz aż dwie niewiadome
x i t.
8 sie 00:29
bezendu: A mój sposób ? post 20:37 ?
8 sie 00:31
Gustlik: Sposób bardzo dobry, Ty ptrzyrównałeś czasy, tylko można było zauważyć, że 3/5=3x, a 2/5=2x,
cała trasa to 5x, czyli x=1/5 trasy i nie byłoby ułamków piętrowych.
Czyli robiąc Twoją metodą zrobiłbym tak:
| 3 | | 2 | |
| = |
| potem na krzyż jak proporcję, dalej już prosto. |
| v+30 | | v | |
8 sie 00:35
bezendu:
Ok dziękuje

8 sie 00:37






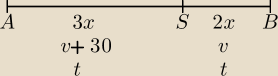 Dwa samochody wyruszyły jednocześnie naprzeciwko siebie z miejscowości A i B.
Prędkość jednego z nich była o 30km/h większa od prędkości drugiego samochodu.
W momencie mijania samochody przejechały odpowiednio 3/5 i 2/5 odległości między
miastami.Oblicz średnie prędkości obu samochodów.
Można bez ułamków, wystarczy trasę podzielić na odcinki 3x zamiast 3/5 i 2x zamiast 2/5:
Oznaczmy:
v − prędkość samochodu B
v+30 − prędkość samochodu A
Ze wzoru s=vt otrzymujemy:
{ 3x = (v+30)t
{ 2x = vt
Dzielimy równania stronami pierwsze przez drugie:
Dwa samochody wyruszyły jednocześnie naprzeciwko siebie z miejscowości A i B.
Prędkość jednego z nich była o 30km/h większa od prędkości drugiego samochodu.
W momencie mijania samochody przejechały odpowiednio 3/5 i 2/5 odległości między
miastami.Oblicz średnie prędkości obu samochodów.
Można bez ułamków, wystarczy trasę podzielić na odcinki 3x zamiast 3/5 i 2x zamiast 2/5:
Oznaczmy:
v − prędkość samochodu B
v+30 − prędkość samochodu A
Ze wzoru s=vt otrzymujemy:
{ 3x = (v+30)t
{ 2x = vt
Dzielimy równania stronami pierwsze przez drugie:
 Gustlik czyli w tego typu zadaniach najpierw zapisujemy stosunek drogi ?
Gustlik czyli w tego typu zadaniach najpierw zapisujemy stosunek drogi ?
