prosze o rozwiazanie atamniemarudz: 1. Dane są proste y= x + m + 2 oraz y= 2x+3m. a) Dla jakich wartości parametru m punkt przecięcia tych prostych należy do obszaru opisanego nierównością |x| + |y| ≤ 4? b) Jaką figurą jest zbiór punktów przecięcia tych prostych dla m ∊ R? 2. Dla jakich wartości parametru m rozwiązaniem układu równań jest para liczb różnych znaków? a) {3x + 2y= m − 1 {x − y = m + 3 b) {2x −5y =22 −5m {−x + 3y = m − 14 3. Rozwiąż układ równań. a) {2x + |y| = 3 {|x| − 2y = 3 b) {|x − y| = 1 {|x + y| = 2 c) {|x − 1| − |y + 1| = 6 {3x + 2y = 3

matura : zadanie 3 rozważ x≥0 x≥<0 y≥0 y<0

Mila: Zadanie 1. Dane są proste y= x + m + 2 oraz y= 2x+3m. 1) Punkt przecięcia prostych: 2x+3m=x+m+2⇔ x=−2m+2 y=−m+4 2) Dla jakich wartości parametru m punkt przecięcia tych prostych należy do obszaru opisanego nierównością |x| + |y| ≤ 4? |x|=|−2m+2|=|2m−2| i |y|=|−m+4|=|m−4| |x|=^df2m−2 dla m≥1 i |y|=m−4 dla m≥4 |x|=−2m+2 dla m<1 i |y|=−m+4 dla m<4 Stąd warunek |x|+|y|≤4 jest równoważny alternatywie warunków: a)m<1

	2
−2m+2−m+4≤4⇔m≥		i m<1
	3

lub b)m∊<1,4) 2m−2−m+4≤4⇔m≤2 i m≥1 lub c) m≥4 2m−2+m−4≤4 3m≤4+4+2 3m≤10

	10
m≤		i m≥4 brak rozwiązań
	3

Odp.

	2
m∊<		,2>
	3

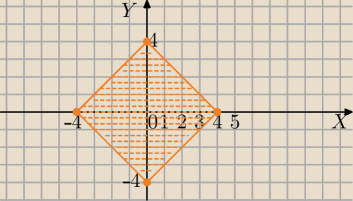
Mila: |x|+|y|≤4