Granica ciagu
Garth:
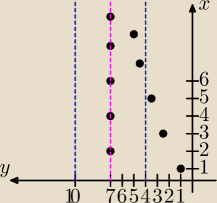
A wiec, zaczalem sie wlasnie uczyc granicy ciagu i chcialbym przedstawic do oceny moje
postrzeganie tego zagadnienia, aby sie upewnic, czy jest ono wlasciwe, czy nie. Posluze sie
wykresem XOY w troche innej perspektywie, niz zazwyczaj oraz przykladowym ciagiem − a
n [nie
okresle go zadnym wzorem].
|a
n −g| < ε
Liczba g jest granica ciagu ⇔ , gdy dla kazdej liczby dodatniej ε prawie wszystkie wyrazy ciagu
a
n znajduja sie w odleglosci mniejszej niz ε od g.
Lub inaczej: liczba g jest granica ciagu (a
n) wtedy i tylko wtedy, gdy dla kazdej liczby
dodatniej ε istnieje taka liczba δ, ze dla kazdej liczby naturalnej n > δ zachodzi nierownosc
|a
n − g| < ε
A wiec w przypadku mojego przykladowego ciagu, co nastepuje:
|a
n − 7| < ε
Jak rozumiem ta nierownosc odnosi sie wylacznie do osi OY.
Granica jest 7 − zbiegaja bowiem do niego wszystkie wartosci ciagu.
ε = 3, − prawie wszystkie wyrazy ciagu znajduja sie w odleglosci mniejszej niz 3 od y = 7
[czyli zawieraja sie w przedziale y∊(4,10)
δ = 5 [tutaj akurat niech bedzie to umowne, bo jak widac na wykresie nie jest to tak idealnie
przedstawione − szkoda, ze nie ma gumki w panelu rysowania

], a wiec wszystkie wyrazy ciagu
wieksze od 5 [czyli a
6, a
7, a
8,...] znajduja sie w odleglosci mniejszej niz ε od g.
Czy jest to poprawne rozumowanie? Troche juz pozno jest, wiec moglem tez zapomniec o czyms
wspomniec, wiec mozliwe, ze jeszcze jutro dorzuce kilka pytan.
Z gory dziekuej za pomoc
5 sie 23:44
Garth: Zapomnialem nakreslic δ na moim wykresie, ale juz jutro to zrobie

5 sie 23:47
fx: Jeżeli uczysz się na studia, a nie idziesz na matematykę to definicja granicy nie jest Tobie
zbytnio potrzebna − wtedy wystarczy sama idea − gdy zbliżamy się do granicy to odległość
między wyrazami maleje.
5 sie 23:50
Garth: No coz, ucze sie na studia i ide wlasnie w pazdzierniku na matematyke [stosowana].

Uznalem, ze w wystarczajacym stopniu nadrobilem zaleglosci [przynajmniej te, ktorych
nienadrobienie skutkowalo by pewna porazka na studiach] ze szkoly sredniej i jestem gotow
zaczac sie uczyc matematyki wyzszej.
5 sie 23:56
6 sie 00:24
Garth: @asdf − wydaje mi sie, ze doskonale to rozumiem i to samo odzwierciedla moj pierwszy post, wiec
albo doszukales sie w nim jakiejs niezgodnosci, albo w ogole go nie czytales tylko po prostu
zalozyles, ze w ogole nie rozumiem tego zagadnienia.

Prosze o wyjasnienie.
6 sie 00:41
asdf: Przyznaje − nie czytałem, bo już mi się literki zlewały od soku (

), dałem po prostu link,
jeżeli to Ciebie w jakis sposob obraziło (nie mialem takich zamiarów i nie powinno) to
przepraszam

6 sie 13:04
Garth: 
Bynajmniej mnie to nie obrazilo, w koncu tez chciales w pewien, mimo, ze nie akurat ten, ktory
byl mi potrzebny, sposob, pomoc.
Chociaz troszke mnie koledzy skolowaliscie, bo z kolei post
fx lekko sugeruje, ze to co
napisalem to kompletna bzdura i wrecz odradza mi jakiekolwiek proby zrozumienia tego
zagadnienia.

Tak wiec pytanie jest jak najbardziej aktualne dla tych, ktorzy chcieli by sie zapoznac z ta
sciana tekstu. Gwoli scislosci − wykres narysowalem w innej perspektywie [tak, ze patrzymy
'naturalnie' na wykres OY, poniewaz sama definicja granicy dotyczy tego wykresu].
6 sie 20:51
asdf: Pamiętam, że na pierwszym kolokwium z granic miałem udowodnic z definicji granicę ciągu, a jej
zrozumienie tylko ułatwia sprawę. Na egzaminie miałem napisać definicję granicy funkcji (z tw.
Hainego) i udowodnić brak granicy..trochę teorii wymagają, a to, że idziesz na studia
matematyczne to zrozumienie takich zagadnien powinno być Twoim "własnym" obowiązkiem. Podobnie
jest z pochodną z definicji − nie trzeba umieć liczyć, bo są już wzory, ale umieć − przydatna
rzecz

6 sie 21:32
asdf: A z definicją granicy ciągu jest taka sprawa, że ona jest zbyt prosta, żeby od razu ją
zrozumieć

tak jest według mnie..bo później się przekonasz, że to banał

6 sie 21:33
Garth: "A z definicją granicy ciągu jest taka sprawa, że ona jest zbyt prosta, żeby od razu ją
zrozumieć tak jest według mnie..bo później się przekonasz, że to banał"
A wiec ostatecznie − moje rozumowanie przedstawione w pierwszym poscie jest bledne?

Prosilbym, w miare mozliwosci, o skorygowanie tego, czego nie rozumiem, bo wydaje mi sie, ze
akurat ja rozumiem.
"na pierwszym kolokwium z granic miałem udowodnic z definicji granicę ciągu" − jak rozumiem,
majac podany przykladowy ciag? Bo sam robilem juz troche takich zadan, co prawda troche
schematycznie, bo mam w ksiazce przedstawiony schemat, no ale nie mialem z tym jakichs
wiekszych trudnosci, natomiast same zadania [jak dotad] na wyznaczenie granicy [oczywiscie na
razie tych prostszych ciagow] robie bezblednie.
6 sie 21:43
asdf: Troche chaotycznie napisales pierwszy post..podeslalem Ci linka i jak tak rozumiesz to ok, jak
chcesz to policz sobie taką granicę:
1. wykazać, że granicą ciągu
a) a
n =
n√5 jest 1
| | 1 | |
2. Udowodnić, że granicą ciągu |
| nie jest 1 |
| | n | |
odpowiedzi:
1. a − n > log
1/2ε
w 1.b − tu należy się komentarz przy opuszczaniu logarytmu, jezeli wiesz o co chodzi, jezeli
nie to podesle rozwiązanie.
6 sie 22:31
Garth: 2. Dowod nie wprost.
n ≥ 1, ε > 0
n−1 < nε
n + nε < 1
n(1 + ε) < 1
| 1 | |
| bedzie zawsze mniejsze lub rowne zeru, co jest sprzeczne z n ≥ 1, poprawnie? |
| 1 + ε | |
6 sie 22:45
Garth: W pierwszym zadaniu szczerze powiedziawszy mam problem z przeksztalceniem potegi w logarytm
[chyba bedzie trzeba powtorzyc sobie logarytmy

].
|
n√5 − 1| < ε
n√5 − 1 < ε
5
1/n =
n√5 < ε + 1
6 sie 22:55
asdf:
miałeś takie coś?
5
1/n < ∊ + 1
log
55
1/n < log
5(∊+1) // tutaj trzeba zaloz od razu, ze logarytm ten jest liczbą
dodatnią(log
(∊+1) > 0, bo ∊> 0, a z wykresu logarytmu, log
5x >0 dla każdego x > 1, więc nie
zmieniamy znaku, ponieważ
6 sie 22:58
asdf: te "ponieważ" nie bierz pod uwage, dopisywalem do srodka zdania, a zapomnialem tamto usunac.
6 sie 22:59
asdf: do zadania drugiego:
tak, nie chcę się czepiać, a jedynie Ci podpowiedzieć

Tu w tym wszystkich teraz chodzi o to,
że te n − punkt/miejsce/moment od ktorego kazde kolejne wyrazy ciagu mieszcza sie w pasku
epsilonowym nie istnieje, ponieważ jest "do momentu", a nie "od momentu", rozumiesz?

6 sie 23:01
asdf: przykładowo, jakby wyszło:
| | 1000000 | |
n < |
| , no to oczywiście znajdę taki epsilon, ktory da wartość większą od 1, ale |
| | 1 + ∊ | |
w definicji jest wyraźnie "dla każdego epsilona", a nie "istnieje taki epsilon"

6 sie 23:04
Garth: Do pierwszego − tak, wlasnie doszedlem do takiego momentu i dalej juz teraz rozumiem, dzieki.

Zaraz sprobuje drugi przyklad z pierwszego rozgryzc − na razie nie dawaj mi gotowca.
Do drugiego zadania − tak, chyba to rozumiem, jedynie wyrazy ciagu mniejsze od jeden [mniejsze
| | 1 | |
dlatego, ze |
| ∊ (0,1> dla kazdego ε > 0], czyli na przyklad a0, a−1, a−2, ... |
| | 1 + ε | |
itd. znajdowaly by sie w tym pasku, jednakze pamietamy, ze ciag jest to funkcja, ktora
przyjmuje wartosci jedynie dla argumentow naturalnych dodatnich.

6 sie 23:10
asdf: Jest taka funkcja "całość z", zapoznasz się z nią na wykładach

Jeżeli jednak chcesz to mogę
ją opisać, która określa dla jakiego epsilona wszystkie wyrazy ciągu (począwszy od pierwszego)
w pasku epsilonowym, a kiedy od jakiegoś wyrazu.
6 sie 23:18
Garth: W odpowiedziach do pierwszego zadania pomieszales tez chyba odpowiedzi? Nie powinny byc
odwrotnie?
Z kolei wyszlo mi troche inaczej dla b)
A u Ciebie wyszlo, ze n > log
1/2ε
Chetnie poslucham o tej funkcji.

I dzieki za dotychczasowa pomoc.
6 sie 23:29
Garth: Aha, i tutaj "która określa dla jakiego epsilona wszystkie wyrazy ciągu (począwszy od
pierwszego)
w pasku epsilonowym, a kiedy od jakiegoś wyrazu." chyba zgubiles czasownik?
6 sie 23:29
ZKS:
To jest to samo.
| | 1 | |
loga |
| = logab−1 = −logab = loga−1b = log1/ab |
| | b | |
6 sie 23:31
Garth: Rzeczywiscie, dzieki, naprawde bede sobie musial powtorzyc logarytmy.

6 sie 23:32
asdf: Zadania z logarytmów mam jeszcze w notatkach z pierwszego semestru, proszę, jak będą za trudne
na początek − nie szkodzi

A jak juz to podesle latwiejszy zestaw:
http://www.speedyshare.com/3wdKu/logarytmy2.JPG
O tej funkcji "całość z" napiszę już jutro
6 sie 23:47
Garth: Dzieki za logarytmy, jutro juz chyba poprobuje, jesli sie nie myle mam przeksztalcic lewa
strone na prawa lub na odwrot?
6 sie 23:53
Garth: No i jeszcze jedno − lg znaczy to samo co log?
6 sie 23:58
fx: lg to oznaczenie log10
6 sie 23:59
asdf: lg(x) = log10(x)
ln(x) = loge(x)
7 sie 00:03
Garth: Racja, chociaz samo log tez jest w sumie uzywane do oznaczenia logarytmu dziesietnego i chyba
po prostu sie juz blednie przyzwyczailem, ze to jedyne jego oznaczenie.

7 sie 00:04
asdf: np w USA log oznacza logarytm naturalny (ln)

7 sie 00:07
fx: Jest wiele takich oznaczeń, które np. za granicą naszego kraju są inne.
Choćby polski tg i ctg − w większości publikacji zagranicznych funkcjonują jako tan i cot.
Podobnie z funkcjami odwrotnymi do trygonometrycznych − u nas − arcsin, arccos, arctg na
zachodzie sin
−1, cos
−1, tan
−1. Funkcje area analogicznie. Dużo takich nieścisłości w
jakże ścisłej matematyce

.
7 sie 00:10
asdf: " jesli sie nie myle mam przeksztalcic lewa strone na prawa lub na odwrot?" − czasem wystarczy
przerzucic na lewą strone, przyrownac do zera, skorzystac z niektorych wlasnosci logarytmu
itd, chodzi o to, zeby nabrac wprawy...jak nie miales za duzo dzialan na logarytmach w szkole
sredniej to Ci podesle latwiejsze zestawy − to będzie chyba troche za trudne, aczkolwiek życzę
Ci powodzenia i wytrwałości

Ja się z tego zestawu nauczylem liczyc logarytmy i nie mialem z
nimi problemu pozniej
7 sie 00:11
Garth: Tzn powiem tak − na pierwszy rzut oka wydaja sie byc dosc trudne, w szkole, czy tez
samodzielnie, rozwiazywalem o wiele latwiejsze na poziomie szkoly sredniej, takze jesli to
mozliwe to prosilbym tez o latwiejszy zestaw, z ktorego moglbym policzyc chociaz kilka na
rozgrzewke przed tymi trudniejszymi [ co i tak, tak jak wspomnialem, nastapi dopiero jutro].

Jutro sprobuje tez popracowac nad tymi trudniejszymi, czy z powodzeniem, czy nie, zobaczymy.

Z tego, co patrzylem, to na pierwszym semestrze mam miec rowniez taki przedmiot jak
"repetytorium z matematyki" i z tego co udalo mi sie dowiedziec bedzie to swojego rodzaju
powtorka ze szkoly sredniej, takze pewnie jeszcze bedzie sie mozna douczyc czegos [podobno
jest tam tez powtorka wlasnie z logarytmow].
Dziekuje

7 sie 00:18
asdf: Można zaliczyć matematykę bez przygotowania się do niej

Mnie się to udało z dużym jak dla
mnie sukcesem, a nic się nie przykładałem w wakacje, więc spokojnie. Repetytorium − nie miałem
takiego czegoś, a oba semestry zaliczone

Dobrze, ze chcesz się teraz czegos pouczyc, bo
pozniej będziesz miec duuuzo lżej. Łatwiejszy zestaw:
http://speedy.sh/4RsZf/Zadania-z-logarytmow-dla-I-roku-Inf.doc
Co do rozwiązań − sprawdzaj z wolframem najlepiej, odpowiedzi często są złe.
7 sie 00:22
fx: Jeżeli chcesz załapać mechanizmy rozwiązywania zadań z logarytmami to polecam "99 zadań o
logarytmach z pełnymi rozwiązaniami krok po kroku". Polecam też pozostałe zeszyty z tej serii
− taki dawny wolframalpha

. Tylko, że masz aż 99 przykładów setep−by−step za jakieś 10
złotych

.
7 sie 00:45
asdf: co do granic:
google.pl → 310 granic krok po kroku
7 sie 00:57
Garth: Logarytmy − z latwiejszego zestawu zrobilem na razie bez wiekszych problemow przyklady b oraz c
z pierwszego zadania oraz a i b z drugiego.
Co do a z pierwszego, dochodze do np. takiego momentu, i nie wiem, co by tu dalej mozna zrobic.
3
x−1+1/x = 4
x−2+1/x
PS, jak w wolframie wpisac pierwiastek wiekszego stopnia niz 2?
A tutaj do sprawdzenia granica, przy czym liczona z pomoca twierdzenia o trzech ciagach.
| 1 | | 1 | | 1 | |
| > |
| > |
| |
| √n2 | | √n2+1 | | √n2+n2 | |
| | 1 | | 1 | | 1 | |
lim |
| = lim |
| = 0 ⇒ lim |
| = 0, poprawnie, czy tez cos tu pokrecilem? |
| | n | | n√2 | | √n2+1 | |
Oczywiscie poza tym widac na pierwszy rzut oka, ze to jest wlasnie granica tego ciagu bez
uzywania twierdzenia, ale chce wiedziec, czy dobrze sie nim posluzylem.
7 sie 10:55
Garth: "PS, jak w wolframie wpisac pierwiastek wiekszego stopnia niz 2?" − juz znalazlem odpowiedz.
7 sie 11:19
asdf: przyjęło się, że od wartości najmniejszych do największych się szacuje, czyli:
| | 1 | | 1 | | 1 | |
reszta ok. Powinno się zapisać |
| = |
| = |
| z komentarzem, że są to |
| | √n2 | | |n| | | n | |
argumenty →
∞ 
U mnie tego wymagała prowadząca, chociaż przy jednym zadaniu zaznaczyć,
dlaczego tak "beztrosko" sobie opuszczam pierwiastki

Później w granicach funkcji trzeba
będzie patrzeć na granice argumentów

7 sie 13:57
asdf: w pierwszym wydaje mi się, że jest błąd, tam powinno być
| | 3 | | 4 | | 9 | |
( |
| )x−1 * ( |
| )1/x = |
| |
| | 4 | | 3 | | 16 | |
to spróbuj policzyć
7 sie 14:01
Garth: To zmienia postac rzeczy, teraz wyszlo mi bezproblemowo.

A tyle sie bawilem z tym blednym.

Natomiast jeszcze sie zastanawiam co do przykladu a z drugiego zadania, bo wychodzi mi odrobine
jedynie, inaczej.
| | 1 | | 1 | |
x > − |
| , a powinno byc chyba: x < − |
| , nie wiem czemu.  |
| | 4 | | 4 | |
7 sie 14:18
7 sie 14:20
Basia: dlatego, że dla a∊(0,1) funkcja f(x) = ax jest malejąca
7 sie 14:22
asdf: tak samo:
loga(x) > loga(x+1) ∀a ∊ (0,1) ⋀ x > 0
7 sie 14:26
Garth: Tez racja, a co znaczy ∀? Spotkalem sie juz z tym symbolem, ale jakos nigdy nie sprawdzilem
jego znaczenia.

Jak zabrac sie do trzeciego przykladu (c) z drugiego zadania z latwiejszego zestawu logarytmow?
Bo cos nie moge sobie poradzic ze wzgledu na te siodemke.

7 sie 21:48
7 sie 21:52
Garth: Mila − chodzi o definicje i istote granicy ciagu?

Tak naprawde zakladajac ten temat juz
wiedzialem [bo nikt nie udowodnil, ze jest inaczej − o co prosilem, w przypadku gdyby tak
bylo], na czym ona polega, ale dzieki mimo wszystko.

7 sie 22:03
Garth: Sama publikacje tez wrzucam do zakladek, wiec tym bardziej dziekuje, bo moze jeszcze mi sie
przyda.


7 sie 22:04
Mila:
Masz tam rozpisane rozwiązanie zadań− badanie granicy z definicji.
7 sie 22:05
Garth: Tak, chociaz juz probowalem to robic i szczerze powiedziawszy zaczalem tez robic przyklad 2.2.2
z tejze wlasnie publikacji [strona wlasnie 48], i sie zatrzymalem na:
| | 1+2ε | |
n > log2 |
| , jak dalej przeksztalcic? Tam juz w sumie chyba niewiele brakuje do konca − |
| | ε | |
7 sie 22:11
Garth: asdf, w logarytmach [dalej latwiejszy zestaw] − zadanie 3, drugi podpunkt z przykladu a,
tam ma byc:
| | √2 | | √28 | |
log( |
| )8, czy log |
| ? |
| | 4 | | 4 | |
7 sie 22:18
asdf:
z postaci: log
ab
8 = b
To zadanie można tak rozwiązać:
log
21/2−28 = log
2−3/28 = log
2−3/22
3 = −2
7 sie 22:29
Mila: ε>0
dla n>1 mianownik jest dodatni i spełniona jest nierówność dla każdego ε>0
2)
| 5−4n2*ε+6ε | |
| <0 i n∊N+ |
| 4n2−6 | |
dla n>1 mianownik jest dodatni
W takim razie :
−4n
2*ε+6ε+5<0 /:(−4ε)
(n−
√6ε+54ε)*(n+
√6ε+54ε)>0⇔
n>
√6ε+54ε rozpatrujesz tylko parabolę po prawej stronie OY, dla n dodatnich
Czy o to chodziło?
7 sie 22:44
Garth: Ojejku, Mila, przepraszam, ja policzylem dla przykladu 2.2.3, co wyszlo mi zreszta dobrze,
takze nie mam pytan co do tego, nawet nie przeczytalem jeszcze co wlasnie odpisalas − zaraz to
zrobie i dodatkowo policze to w przykladzie 2.2.2, zeby sprawdzic, czy bede umial, jak nie to
jeszcze dam znac. Dzieki jeszcze raz i przepraszam za klopot

7 sie 22:50
Mila:
Do logarytmu podstawiasz konkretne ε.
Np.
3=log
28<log
2(12)<log
2(16)=4
stąd n>4
7 sie 22:56
Garth:
Dany jest ciag okreslony rekurencyjnie.
{a
1 = 3
| | an−1 + 2 | |
{an = |
| dla n > 1 |
| | 3 | |
| | 3n−1 + 2 | |
Wykaz, ze wzor ogolny ma postac an = |
| , a nastepnie oblicz jego granice. |
| | 3n−1 | |
1.
n = 1 ⇒ an = 3
2. dla kazdego n > 1
| | 3n−1 + 2 | | 3n + 2 | |
[an = |
| ⇒ an+1 = |
| |
| | 3n−1 | | 3n | |
| | 3n + 2 | | 3n−1 * 3 + 2 | |
an+1 = |
| = |
| = |
| | 3n | | 3n−1 * 3 | |
| 3 | | 3n−1 + 2 | | 4 | | 3 | | 4 | |
| * |
| − |
| = |
| * an − |
| = |
| 3 | | 3n−1 | | 3n | | 3 | | 3n | |
| | 4 | | an−1 + 2 | | 4 | |
an − |
| = |
| − |
| = ...? |
| | 3n | | 3 | | 3n | |
I jak dalej przeksztalcic? A moze w ogole zle sie za to zabieram?
asdf − wieczorem chyba jeszcze sie wezme za te logarytmy, troche wolno mi to idzie bo
glownie ucze sie granic, jesli Cie to zbytnio meczy, to powiedz, a przestane.

9 sie 13:45
asdf: Nie męczysz mnie

To co teraz robisz to jest rekurencja, czyli musisz rozpisać kilka wyrazów
tego ciągu, podam Tobie przyklad, a Ty rozpiszesz swój ciąg.
Np.
a
n = a
n−1 + n
a
1 = 3
a
n = a
n−1 + n = (rekurencja) a
n−2 + n + n−1 = (rekurencja) a
n−3 + n+n−1 + n − 3 =
(uporządkowuje) = a
n−3 + 3n − 4 = (rekurencja) a
n−4 + 3n − 4 + n − 3 = (uporzadkowuje)
a
n−4 + 4n − 7
= (rekurencja) a
n−5 + 4n − 7 + n − 4 = (uporzadkowuje) a
n−5 + 5n − 11 = ... a
n−k + kn
− (2k −1)
dla n − k = 1 otrzymujemy n = k+1
a
1 + k*(k+1) − (2k−1) =3 + k
2 + k − 2k + 1 = k
2 − k + 4
coś takiego..jak się nie pogubiłem to jest ok, później to sprawdzę, bo teraz muszę znikac i
chciałem Ci tylko na szybkiego wytlumaczyc o co w tym chodzi

~15:30 wróce i sprawdze czy
dobrze to zrobilem.
9 sie 14:12
asdf: oczywiscie tu powinno byc odwolanie do zmiennej n, a nie k, więc spróbuj teraz sam:
n −k = 1
−k = 1−n
k = n−1
za k podstaw "n−1"
9 sie 14:16
asdf: jest wiele sposobow dowodzenia tego, ja teraz spadam, pozniej Tobie pomoge.
9 sie 14:18
Garth: W Twoim przykladzie chyba powinno byc:
an−2 +2n −1 = an−3 + 3n − 3 = an−4 + 4n −6?
9 sie 14:55
Garth:
Przy zalozeniu, ze a
n = a
n−k + kn − (2k − 1) jest prawdziwe [a smiem twierdzic, ze w tym
przykladzie nie jest

]:
a
n = n
2 − 3n + 7 ⇒ a
1 ≠ 3, czyli chyba rzeczywiscie sie pomyliles, ale sama istote problemu
zdolales mi mniej wiecej przyblizyc mimo tego.
9 sie 15:16
asdf: tak, są wakacje, ja na razie odpoczywam i nie chce mi sie za bardzo myśleć

Od nastepnego
tygodnia dopiero ruszam, na razie ciesze się wolnością

9 sie 15:37
Garth: Co wiec powinno byc na miejscu (2k − 1)? Bo jakos nie moge nic wymyslic.

9 sie 15:39
use: @garth a gdzie na studia idziesz

9 sie 15:54
Garth: Ide u siebie na miejscu − Politechnika Rzeszowska, wiec poziom raczej nie jakis bardzo wybitny.

9 sie 15:55
9 sie 16:02
fx: Nie zauważyłem aby ktoś odpowiedział autorowi jak wpisać pierwiastek dowolnego stopnia do
wolframa.
Odpowiadam:
x1/n = pierwiastek stopnia n z x.
9 sie 16:06
Garth: @fx znalazlem juz wowczas sam, o czym zaraz po tym powiadomilem w kolejnym poscie. Chociaz
sam znalazlem formule − n−th root of k
9 sie 16:10
Garth: Rozpisalem sobie ten moj przyklad.
| | 3n−1 + 2 | |
A mialem do udowodnienia, ze wzor ogolny wyglada tak: |
| |
| | 3n−1 | |
{a
1 = 3
| | an−1 + 2 | |
{an = |
| dla n > 1 |
| | 3 | |
| | an−1 + 2 | | an−2 + 8 | | an−3 + 26 | | an−4 + 80 | |
an = |
| = |
| = |
| = |
| = |
| | 3 | | 9 | | 27 | | 81 | |
| | an−5 + 242 | | an−k + 3k − 1 | |
|
| = |
| |
| | 243 | | 3k | |
n − k = 1 ⇒ k = n − 1
| a1 + 3n−1 − 1 | | 3 + 3n−1 − 2 | |
| = |
| = |
| 3n−1 | | 3n−1 | |
| | 3n−1 + 1 | | 3n−1 + 2 | |
= |
| ≠ |
| |
| | 3n−1 | | 3n−1 | |
Pomocy

I dzieki zarazem

9 sie 17:30
Garth: Oho, teraz przy czytaniu to zauwazylem. Moze powinienem rzeczywiscie sobie zrobic przerwe od
tej nauki, szczegolnie w taka pogode.
| | a1 + 3n−1 − 1 | | 3 + 3n−1 − 2 | |
Z |
| zrobilem |
| − co jest nieprawda, a po |
| | 3n−1 | | 3n−1 | |
poprawce okazuje sie, ze zadanie dobrze jest zrobione. A na egzaminie trzeba by cos jeszcze
dopisywac, czy taki dowod by wystarczyl?
9 sie 17:33
Godzio:
Dowód indukcyjny (chyba najłatwiej)
Dla n = 1, oczywiste
Załóżmy, że zachodzi dla pewnego n, dowiedziemy, że zachodzi również dla n + 1
| | 3n − 1 + 2 | | 3n + 2 | |
an = |
| ⇒ an + 1 = |
| |
| | 3n − 1 | | 3n | |
| | 3n − 1 + 2 * 3n − 1 + 2 | | 3n + 2 | |
= |
| = |
| |
| | 3n | | 3n | |
= korzystamy z założenia
To co Ty zrobiłeś to nie jest dowód, a jedynie przypuszczenie, że tak jest. Jednakże nie wiem
gdze u Ciebie tkwi błąd.
9 sie 17:43
Garth: Ten blad juz znalazlem − opisalem go w kolejnym poscie o godzinie 17:33.
Na poczatku probowalem wlasnie indukcja, co widac kilka postow wczesniej. Co do Twojego dowodu,
to rozumiem cale przeksztalcenie, ale nie wiem jedynie, skad sie wziel ten poczatek: a
n+1 =
9 sie 17:51
Godzio:
To jest ze wzoru rekurencyjnego. (post wysłałem zanim zobaczyłem, że napisałeś

)
9 sie 17:54
Garth: Rzeczywiscie. Teraz juz wszystko rozumiem, dzieki wielkie.

9 sie 17:55
Garth: Wracajac do latwiejszego zestawu logarytmow, za ktory wlasnie sie zabralem.
10
2+2log7 = 10
2 * 10
log49 = 100 * 49 = 4900.
Natomiast Wolfram|Alpha twierdzi, ze jest to liczba niewymierna, ktorej przyblizenie wyglada
tak:
779507.50003375627004605122716681668973886634782383746
http://www.wolframalpha.com/input/?i=10%5E%282%2B2log7%29
Co robie nie tak?
9 sie 19:58
9 sie 20:00
ICSP: Albo naucz się używać wolframa, albo z niego nie korzystaj.
9 sie 20:01
Garth: :( − ucze sie. A nauczenie sie uzywania go wymaga wlasnie uzywania go.
9 sie 20:04
fx: http://www.etrapez.pl/wolframalpha/
Jeżeli zapiszesz się na newletter otrzymasz całkiem przyjazne opracowanie traktujące o
wykorzystaniu wolframa do komputerowego wsparcia obliczeń (również a może przede wszystkim −
symbolicznych).
9 sie 20:27
Garth: Dziekuje.
9 sie 20:30
9 sie 20:52
fx: Mianownik musi być różny od zera.
9 sie 21:08
Garth:
log10(5x−4) ≠ 0
5x−4≠1
x≠1, dzieki, ja nadal zapominam, ze nie dzielimy przez zero!
9 sie 21:12
Garth:
5
x+3 < 25 * 7
−x−1 ⇔
| | 1 | |
⇔ 5x+3 < 52 * ( |
| )x−1 ⇔ |
| | 7 | |
⇔ ...
Ma ktos jakies pomysly na ten przyklad?
9 sie 21:26
9 sie 21:29
9 sie 21:38
Garth:
35 * 35x < 1 ⇔
⇔ 35x < 35−1
⇔ x < −1, dobrze? W jakich sytuacjach zmienia sie znak przy takich obliczeniach?
9 sie 21:43
Mila:
Na ogół tak rozwiązujemy.
35x+1<1⇔
35x+1<350 funkcja wykładnicza rosnąca⇔
x+1<0
x<−1
9 sie 21:48
asdf:
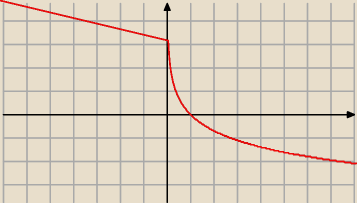
"W jakich sytuacjach zmienia sie znak przy takich obliczeniach?"
W sytuacjach gdy funkja jest malejąca, czyli:
log
a(b), a ∊ (0,1), b > 0
Przykład:
log
1e(x)
| | 1 | | 1 | |
(a = |
| , e ≈ 2,7, czyli |
| < 1) jak widać jest to funkcja malejąca  |
| | e | | 2,7 | |
10 sie 11:03
asdf:
jeszcze są funkcje cyklometryczne, np.
y = arcctg(x),
y = arccos(x)
W takich przypadkach też trzeba pamiętać o znaku przy rozwiązywaniu nierówności.
10 sie 11:05
Garth: Do zadania z godziny 13:45 z wczoraj, ktorego przeciez zapomnialem dokonczyc, bylo tam bowiem w
drugiej czesci obliczyc granice tegoz ciagu.
Oczywiscie udowodnilismy juz, ze powyzszy wzor jest prawdziwy, a wiec:
| | 3n:3 + 2 | | | |
liman = lim |
| = lim |
| = 1 |
| | 3n : 3 | | | |
Poprawnie?
Z gory dzieki
10 sie 22:31
asdf: tak, mozesz od razu 3
n−1 przed nawias, ale też jest ok

10 sie 23:04
Garth: Dalej te logarytmy z latwiejszego zestawu.
Zadanie 5. przyklad g.
Jest tam log
23x, co zrobic z tym fantem? Probowalem podzielic cale wyrazenie przez log
3x,
ale pozniej nic nie wymysillem.

10 sie 23:46
asdf:
log23x + log3x3 + 2 = 0
log23x + 3log3x + 2 = 0
t = log3x
10 sie 23:59
asdf: P.S pamiętaj zawsze o dziedzinie.
11 sie 00:02
Garth: Chyba cos mi nie wychodzi.
D: x > 0
log
3x = t
t
2 + 3t + 2 = 0
(t+1)(t+2) = 0
log
3(x+1)=0 v log
3(x+2)=0
x + 1 = 1 v x + 2 = 1
(x = 0 v x = −1) ∉ D
Ale moze jakis strasznie glupi blad popelniam, juz nie mam nawet sily szukac.

Dzieki za
pomoc i dobrej nocy zycze, juz pewnie 'dzisiaj' tu nie zajrze.

11 sie 00:11
asdf:
t+1 = 0 ⇒ t = −1 ⇒ log3x = −1 ⇒ (z definicji) 3−1 = x
t+2 = 0 ⇒ t = −2 ⇒....
11 sie 00:19
asdf:
dlaczego ty za x wstawiasz x+1?
t = log3x, czyli t+1 = 0 ⇒ log3x +1 = 0
11 sie 00:20
Garth: Sam nie wiem, skad mi tam cos takiego wyszlo.

Wyszedlem z pracy wczoraj o 22, a to jeszcze bylo kolo polnocy, wiec juz chyba mialem prawo
pisac takie glupoty.

t = log
3x
(t + 1)(t + 2) = 0
log
3x = −1 v log
3x = −2
11 sie 21:47
asdf: brawo

jeszcze kilka przykladow i kolejny zestaw
11 sie 22:10
Garth: Tak, chociaz nierownosci na razie nie robilem − w szkole nie bylo, sam tez nigdy nie
rozwiazywalem, wiec wpierw poczytam sobie na ten temat w ksiazce − ale to juz jutro. Dokoncze
zaraz chyba te ostatnie przyklady z piatego zadania. Niestety praca nie pozwala mi uczyc sie
tyle, ile bym chcial.

Dopiero od pazdziernika bede mogl sie calkowicie poswiecic matematyce.

I moze tez troszke
innym zajeciom.
11 sie 22:19
Garth: | | 1 | |
log(2x + 4x) − log8 = log(2x−1 − |
| ) |
| | 4 | |
D:
2
x + 2
2x > 0 ⇔ ...?
| | 1 | | 1 | | 1 | |
2x−1 > |
| ⇔ 2x > |
| ⇔ log22x > log2 |
| ⇔ x > −1 |
| | 4 | | 2 | | 2 | |
11 sie 22:29
asdf: troche nakombinowałeś

ale też dobrze
D:
2
x + 4
x > 0 zawsze

2
x−1 > 2
−2
x−1 > −2
x > −1
11 sie 22:40
asdf: a poradziłeś sobie z tą równością?
11 sie 22:48
Garth: Probuje ja rozgryzc. :
Na razie tyle wymyslilem:
| | 1 | | 2x+4x | | 1 | |
log(2x + 4x) − log8 = log(2x−1 − |
| ) ⇔ log |
| = log2x−1 − |
| ⇔ |
| | 4 | | 8 | | 4 | |
| | 2x | | 22x | | 1 | |
⇔ log( |
| + |
| ) = log2x−1 − |
| ⇔ |
| | 23 | | 23 | | 4 | |
⇔ log(2
x−3 + 2
2x−3) = log2
x−1 −2
−2 ⇔ ...
Ale chyba bede musial sprobowac inaczej.

11 sie 22:59
Mila:
| | 1 | | 2x+22x | |
Dlaczego opuściłeś nawias , ma byc: log(2x−1− |
| )=log |
| |
| | 4 | | 8 | |
stąd:
| | 1 | | 2x+22x | |
2x−1− |
| = |
| /*23 |
| | 4 | | 23 | |
dokończ
11 sie 23:13
asdf:
| | b | |
logab − logac = loga( |
| ), pozniej to * c i juz masz prawie gotowe  |
| | c | |
11 sie 23:19
Garth: Rzeczywiscie naknocilem, i pozniej od poczatku probowalem, z tym, ze log8 przerzucilem na prawa
strone i doszedlem wlasnie do tego:
2
x +2
2x − 2
x+2 = −2
Czy tak by dalej nie moglo byc (sprobuje tez zaraz za pomoca Twojego wzoru
asdf)?
2
x + 2
2x + 2
1 = 2
x+2
log
22
x + log
22
2x + log
22
1 = log
22
x+2
| | 1 | |
x + 2x + 1 = x + 2 ⇒ x = |
| |
| | 2 | |
11 sie 23:25
11 sie 23:28
Garth: | | 1 | |
log(2x−3 + 22x−3) = log(2x−1 − |
| ) |
| | 4 | |
2
x−3 + 2
2x−3 = 2
x−1 − 2
−2 
11 sie 23:35
asdf: już jutro Ci napisze rozwiązanie, nie chce mi sie teraz liczyc.
12 sie 00:23
Mila:
cd mojego postu z 23:13
Mnożę obie strony równania przez 2
3⇔
2
3*2
x−1−2=2
x+2
2x⇔
2
x+2−2=2
x+2
2x
2
x+2
2x−4*2
x+2=0 [2
x+2=2
x*2
2=4*2
x]
2
2x−3*2
x+2=0
2
x=t, t>0
t
2−3t+2=0
Δ=1
| | 3+1 | | 3−1 | |
t= |
| =2 lub t= |
| =1 |
| | 2 | | 2 | |
2
x=2 lub 2
x=1
2
x=2
1 lub 2
x=2
0
x=1 lub x=0
sprawdź z założeniami.
12 sie 16:01
 A wiec, zaczalem sie wlasnie uczyc granicy ciagu i chcialbym przedstawic do oceny moje
postrzeganie tego zagadnienia, aby sie upewnic, czy jest ono wlasciwe, czy nie. Posluze sie
wykresem XOY w troche innej perspektywie, niz zazwyczaj oraz przykladowym ciagiem − an [nie
okresle go zadnym wzorem].
|an −g| < ε
Liczba g jest granica ciagu ⇔ , gdy dla kazdej liczby dodatniej ε prawie wszystkie wyrazy ciagu
an znajduja sie w odleglosci mniejszej niz ε od g.
Lub inaczej: liczba g jest granica ciagu (an) wtedy i tylko wtedy, gdy dla kazdej liczby
dodatniej ε istnieje taka liczba δ, ze dla kazdej liczby naturalnej n > δ zachodzi nierownosc
|an − g| < ε
A wiec w przypadku mojego przykladowego ciagu, co nastepuje:
|an − 7| < ε
Jak rozumiem ta nierownosc odnosi sie wylacznie do osi OY.
Granica jest 7 − zbiegaja bowiem do niego wszystkie wartosci ciagu.
ε = 3, − prawie wszystkie wyrazy ciagu znajduja sie w odleglosci mniejszej niz 3 od y = 7
[czyli zawieraja sie w przedziale y∊(4,10)
δ = 5 [tutaj akurat niech bedzie to umowne, bo jak widac na wykresie nie jest to tak idealnie
przedstawione − szkoda, ze nie ma gumki w panelu rysowania
A wiec, zaczalem sie wlasnie uczyc granicy ciagu i chcialbym przedstawic do oceny moje
postrzeganie tego zagadnienia, aby sie upewnic, czy jest ono wlasciwe, czy nie. Posluze sie
wykresem XOY w troche innej perspektywie, niz zazwyczaj oraz przykladowym ciagiem − an [nie
okresle go zadnym wzorem].
|an −g| < ε
Liczba g jest granica ciagu ⇔ , gdy dla kazdej liczby dodatniej ε prawie wszystkie wyrazy ciagu
an znajduja sie w odleglosci mniejszej niz ε od g.
Lub inaczej: liczba g jest granica ciagu (an) wtedy i tylko wtedy, gdy dla kazdej liczby
dodatniej ε istnieje taka liczba δ, ze dla kazdej liczby naturalnej n > δ zachodzi nierownosc
|an − g| < ε
A wiec w przypadku mojego przykladowego ciagu, co nastepuje:
|an − 7| < ε
Jak rozumiem ta nierownosc odnosi sie wylacznie do osi OY.
Granica jest 7 − zbiegaja bowiem do niego wszystkie wartosci ciagu.
ε = 3, − prawie wszystkie wyrazy ciagu znajduja sie w odleglosci mniejszej niz 3 od y = 7
[czyli zawieraja sie w przedziale y∊(4,10)
δ = 5 [tutaj akurat niech bedzie to umowne, bo jak widac na wykresie nie jest to tak idealnie
przedstawione − szkoda, ze nie ma gumki w panelu rysowania  ], a wiec wszystkie wyrazy ciagu
wieksze od 5 [czyli a6, a7, a8,...] znajduja sie w odleglosci mniejszej niz ε od g.
Czy jest to poprawne rozumowanie? Troche juz pozno jest, wiec moglem tez zapomniec o czyms
wspomniec, wiec mozliwe, ze jeszcze jutro dorzuce kilka pytan.
Z gory dziekuej za pomoc
], a wiec wszystkie wyrazy ciagu
wieksze od 5 [czyli a6, a7, a8,...] znajduja sie w odleglosci mniejszej niz ε od g.
Czy jest to poprawne rozumowanie? Troche juz pozno jest, wiec moglem tez zapomniec o czyms
wspomniec, wiec mozliwe, ze jeszcze jutro dorzuce kilka pytan.
Z gory dziekuej za pomoc

 Uznalem, ze w wystarczajacym stopniu nadrobilem zaleglosci [przynajmniej te, ktorych
nienadrobienie skutkowalo by pewna porazka na studiach] ze szkoly sredniej i jestem gotow
zaczac sie uczyc matematyki wyzszej.
Uznalem, ze w wystarczajacym stopniu nadrobilem zaleglosci [przynajmniej te, ktorych
nienadrobienie skutkowalo by pewna porazka na studiach] ze szkoly sredniej i jestem gotow
zaczac sie uczyc matematyki wyzszej.

 Prosze o wyjasnienie.
Prosze o wyjasnienie.
 ), dałem po prostu link,
jeżeli to Ciebie w jakis sposob obraziło (nie mialem takich zamiarów i nie powinno) to
przepraszam
), dałem po prostu link,
jeżeli to Ciebie w jakis sposob obraziło (nie mialem takich zamiarów i nie powinno) to
przepraszam 
 Bynajmniej mnie to nie obrazilo, w koncu tez chciales w pewien, mimo, ze nie akurat ten, ktory
byl mi potrzebny, sposob, pomoc.
Chociaz troszke mnie koledzy skolowaliscie, bo z kolei post fx lekko sugeruje, ze to co
napisalem to kompletna bzdura i wrecz odradza mi jakiekolwiek proby zrozumienia tego
zagadnienia.
Bynajmniej mnie to nie obrazilo, w koncu tez chciales w pewien, mimo, ze nie akurat ten, ktory
byl mi potrzebny, sposob, pomoc.
Chociaz troszke mnie koledzy skolowaliscie, bo z kolei post fx lekko sugeruje, ze to co
napisalem to kompletna bzdura i wrecz odradza mi jakiekolwiek proby zrozumienia tego
zagadnienia.  Tak wiec pytanie jest jak najbardziej aktualne dla tych, ktorzy chcieli by sie zapoznac z ta
sciana tekstu. Gwoli scislosci − wykres narysowalem w innej perspektywie [tak, ze patrzymy
'naturalnie' na wykres OY, poniewaz sama definicja granicy dotyczy tego wykresu].
Tak wiec pytanie jest jak najbardziej aktualne dla tych, ktorzy chcieli by sie zapoznac z ta
sciana tekstu. Gwoli scislosci − wykres narysowalem w innej perspektywie [tak, ze patrzymy
'naturalnie' na wykres OY, poniewaz sama definicja granicy dotyczy tego wykresu].

 tak jest według mnie..bo później się przekonasz, że to banał
tak jest według mnie..bo później się przekonasz, że to banał 
 Prosilbym, w miare mozliwosci, o skorygowanie tego, czego nie rozumiem, bo wydaje mi sie, ze
akurat ja rozumiem.
"na pierwszym kolokwium z granic miałem udowodnic z definicji granicę ciągu" − jak rozumiem,
majac podany przykladowy ciag? Bo sam robilem juz troche takich zadan, co prawda troche
schematycznie, bo mam w ksiazce przedstawiony schemat, no ale nie mialem z tym jakichs
wiekszych trudnosci, natomiast same zadania [jak dotad] na wyznaczenie granicy [oczywiscie na
razie tych prostszych ciagow] robie bezblednie.
Prosilbym, w miare mozliwosci, o skorygowanie tego, czego nie rozumiem, bo wydaje mi sie, ze
akurat ja rozumiem.
"na pierwszym kolokwium z granic miałem udowodnic z definicji granicę ciągu" − jak rozumiem,
majac podany przykladowy ciag? Bo sam robilem juz troche takich zadan, co prawda troche
schematycznie, bo mam w ksiazce przedstawiony schemat, no ale nie mialem z tym jakichs
wiekszych trudnosci, natomiast same zadania [jak dotad] na wyznaczenie granicy [oczywiscie na
razie tych prostszych ciagow] robie bezblednie.
 ].
| n√5 − 1| < ε
n√5 − 1 < ε
51/n = n√5 < ε + 1
].
| n√5 − 1| < ε
n√5 − 1 < ε
51/n = n√5 < ε + 1
 Tu w tym wszystkich teraz chodzi o to,
że te n − punkt/miejsce/moment od ktorego kazde kolejne wyrazy ciagu mieszcza sie w pasku
epsilonowym nie istnieje, ponieważ jest "do momentu", a nie "od momentu", rozumiesz?
Tu w tym wszystkich teraz chodzi o to,
że te n − punkt/miejsce/moment od ktorego kazde kolejne wyrazy ciagu mieszcza sie w pasku
epsilonowym nie istnieje, ponieważ jest "do momentu", a nie "od momentu", rozumiesz? 

 Zaraz sprobuje drugi przyklad z pierwszego rozgryzc − na razie nie dawaj mi gotowca.
Do drugiego zadania − tak, chyba to rozumiem, jedynie wyrazy ciagu mniejsze od jeden [mniejsze
Zaraz sprobuje drugi przyklad z pierwszego rozgryzc − na razie nie dawaj mi gotowca.
Do drugiego zadania − tak, chyba to rozumiem, jedynie wyrazy ciagu mniejsze od jeden [mniejsze

 Jeżeli jednak chcesz to mogę
ją opisać, która określa dla jakiego epsilona wszystkie wyrazy ciągu (począwszy od pierwszego)
w pasku epsilonowym, a kiedy od jakiegoś wyrazu.
Jeżeli jednak chcesz to mogę
ją opisać, która określa dla jakiego epsilona wszystkie wyrazy ciągu (począwszy od pierwszego)
w pasku epsilonowym, a kiedy od jakiegoś wyrazu.
 I dzieki za dotychczasowa pomoc.
I dzieki za dotychczasowa pomoc.

 A jak juz to podesle latwiejszy zestaw:
http://www.speedyshare.com/3wdKu/logarytmy2.JPG
O tej funkcji "całość z" napiszę już jutro
A jak juz to podesle latwiejszy zestaw:
http://www.speedyshare.com/3wdKu/logarytmy2.JPG
O tej funkcji "całość z" napiszę już jutro


 .
.
 Ja się z tego zestawu nauczylem liczyc logarytmy i nie mialem z
nimi problemu pozniej
Ja się z tego zestawu nauczylem liczyc logarytmy i nie mialem z
nimi problemu pozniej
 Jutro sprobuje tez popracowac nad tymi trudniejszymi, czy z powodzeniem, czy nie, zobaczymy.
Jutro sprobuje tez popracowac nad tymi trudniejszymi, czy z powodzeniem, czy nie, zobaczymy.  Z tego, co patrzylem, to na pierwszym semestrze mam miec rowniez taki przedmiot jak
"repetytorium z matematyki" i z tego co udalo mi sie dowiedziec bedzie to swojego rodzaju
powtorka ze szkoly sredniej, takze pewnie jeszcze bedzie sie mozna douczyc czegos [podobno
jest tam tez powtorka wlasnie z logarytmow].
Dziekuje
Z tego, co patrzylem, to na pierwszym semestrze mam miec rowniez taki przedmiot jak
"repetytorium z matematyki" i z tego co udalo mi sie dowiedziec bedzie to swojego rodzaju
powtorka ze szkoly sredniej, takze pewnie jeszcze bedzie sie mozna douczyc czegos [podobno
jest tam tez powtorka wlasnie z logarytmow].
Dziekuje 
 Mnie się to udało z dużym jak dla
mnie sukcesem, a nic się nie przykładałem w wakacje, więc spokojnie. Repetytorium − nie miałem
takiego czegoś, a oba semestry zaliczone
Mnie się to udało z dużym jak dla
mnie sukcesem, a nic się nie przykładałem w wakacje, więc spokojnie. Repetytorium − nie miałem
takiego czegoś, a oba semestry zaliczone  Dobrze, ze chcesz się teraz czegos pouczyc, bo
pozniej będziesz miec duuuzo lżej. Łatwiejszy zestaw:
http://speedy.sh/4RsZf/Zadania-z-logarytmow-dla-I-roku-Inf.doc
Co do rozwiązań − sprawdzaj z wolframem najlepiej, odpowiedzi często są złe.
Dobrze, ze chcesz się teraz czegos pouczyc, bo
pozniej będziesz miec duuuzo lżej. Łatwiejszy zestaw:
http://speedy.sh/4RsZf/Zadania-z-logarytmow-dla-I-roku-Inf.doc
Co do rozwiązań − sprawdzaj z wolframem najlepiej, odpowiedzi często są złe.
 . Tylko, że masz aż 99 przykładów setep−by−step za jakieś 10
złotych
. Tylko, że masz aż 99 przykładów setep−by−step za jakieś 10
złotych  .
.
 U mnie tego wymagała prowadząca, chociaż przy jednym zadaniu zaznaczyć,
dlaczego tak "beztrosko" sobie opuszczam pierwiastki
U mnie tego wymagała prowadząca, chociaż przy jednym zadaniu zaznaczyć,
dlaczego tak "beztrosko" sobie opuszczam pierwiastki  Później w granicach funkcji trzeba
będzie patrzeć na granice argumentów
Później w granicach funkcji trzeba
będzie patrzeć na granice argumentów 
 A tyle sie bawilem z tym blednym.
A tyle sie bawilem z tym blednym.
 Natomiast jeszcze sie zastanawiam co do przykladu a z drugiego zadania, bo wychodzi mi odrobine
jedynie, inaczej.
Natomiast jeszcze sie zastanawiam co do przykladu a z drugiego zadania, bo wychodzi mi odrobine
jedynie, inaczej.

 Jak zabrac sie do trzeciego przykladu (c) z drugiego zadania z latwiejszego zestawu logarytmow?
Bo cos nie moge sobie poradzic ze wzgledu na te siodemke.
Jak zabrac sie do trzeciego przykladu (c) z drugiego zadania z latwiejszego zestawu logarytmow?
Bo cos nie moge sobie poradzic ze wzgledu na te siodemke. 
 Tak naprawde zakladajac ten temat juz
wiedzialem [bo nikt nie udowodnil, ze jest inaczej − o co prosilem, w przypadku gdyby tak
bylo], na czym ona polega, ale dzieki mimo wszystko.
Tak naprawde zakladajac ten temat juz
wiedzialem [bo nikt nie udowodnil, ze jest inaczej − o co prosilem, w przypadku gdyby tak
bylo], na czym ona polega, ale dzieki mimo wszystko. 





 To co teraz robisz to jest rekurencja, czyli musisz rozpisać kilka wyrazów
tego ciągu, podam Tobie przyklad, a Ty rozpiszesz swój ciąg.
Np.
an = an−1 + n
a1 = 3
an = an−1 + n = (rekurencja) an−2 + n + n−1 = (rekurencja) an−3 + n+n−1 + n − 3 =
(uporządkowuje) = an−3 + 3n − 4 = (rekurencja) an−4 + 3n − 4 + n − 3 = (uporzadkowuje)
an−4 + 4n − 7
= (rekurencja) an−5 + 4n − 7 + n − 4 = (uporzadkowuje) an−5 + 5n − 11 = ... an−k + kn
− (2k −1)
dla n − k = 1 otrzymujemy n = k+1
a1 + k*(k+1) − (2k−1) =3 + k2 + k − 2k + 1 = k2 − k + 4
coś takiego..jak się nie pogubiłem to jest ok, później to sprawdzę, bo teraz muszę znikac i
chciałem Ci tylko na szybkiego wytlumaczyc o co w tym chodzi
To co teraz robisz to jest rekurencja, czyli musisz rozpisać kilka wyrazów
tego ciągu, podam Tobie przyklad, a Ty rozpiszesz swój ciąg.
Np.
an = an−1 + n
a1 = 3
an = an−1 + n = (rekurencja) an−2 + n + n−1 = (rekurencja) an−3 + n+n−1 + n − 3 =
(uporządkowuje) = an−3 + 3n − 4 = (rekurencja) an−4 + 3n − 4 + n − 3 = (uporzadkowuje)
an−4 + 4n − 7
= (rekurencja) an−5 + 4n − 7 + n − 4 = (uporzadkowuje) an−5 + 5n − 11 = ... an−k + kn
− (2k −1)
dla n − k = 1 otrzymujemy n = k+1
a1 + k*(k+1) − (2k−1) =3 + k2 + k − 2k + 1 = k2 − k + 4
coś takiego..jak się nie pogubiłem to jest ok, później to sprawdzę, bo teraz muszę znikac i
chciałem Ci tylko na szybkiego wytlumaczyc o co w tym chodzi  ~15:30 wróce i sprawdze czy
dobrze to zrobilem.
~15:30 wróce i sprawdze czy
dobrze to zrobilem.
 ]:
an = n2 − 3n + 7 ⇒ a1 ≠ 3, czyli chyba rzeczywiscie sie pomyliles, ale sama istote problemu
zdolales mi mniej wiecej przyblizyc mimo tego.
]:
an = n2 − 3n + 7 ⇒ a1 ≠ 3, czyli chyba rzeczywiscie sie pomyliles, ale sama istote problemu
zdolales mi mniej wiecej przyblizyc mimo tego.
 Od nastepnego
tygodnia dopiero ruszam, na razie ciesze się wolnością
Od nastepnego
tygodnia dopiero ruszam, na razie ciesze się wolnością 




 I dzieki zarazem
I dzieki zarazem 
 )
)

 "W jakich sytuacjach zmienia sie znak przy takich obliczeniach?"
W sytuacjach gdy funkja jest malejąca, czyli:
loga(b), a ∊ (0,1), b > 0
Przykład:
log1e(x)
"W jakich sytuacjach zmienia sie znak przy takich obliczeniach?"
W sytuacjach gdy funkja jest malejąca, czyli:
loga(b), a ∊ (0,1), b > 0
Przykład:
log1e(x)

 jeszcze są funkcje cyklometryczne, np. y = arcctg(x), y = arccos(x)
W takich przypadkach też trzeba pamiętać o znaku przy rozwiązywaniu nierówności.
jeszcze są funkcje cyklometryczne, np. y = arcctg(x), y = arccos(x)
W takich przypadkach też trzeba pamiętać o znaku przy rozwiązywaniu nierówności.


 Dzieki za
pomoc i dobrej nocy zycze, juz pewnie 'dzisiaj' tu nie zajrze.
Dzieki za
pomoc i dobrej nocy zycze, juz pewnie 'dzisiaj' tu nie zajrze. 
 Wyszedlem z pracy wczoraj o 22, a to jeszcze bylo kolo polnocy, wiec juz chyba mialem prawo
pisac takie glupoty.
Wyszedlem z pracy wczoraj o 22, a to jeszcze bylo kolo polnocy, wiec juz chyba mialem prawo
pisac takie glupoty.  t = log3x
(t + 1)(t + 2) = 0
log3x = −1 v log3x = −2
t = log3x
(t + 1)(t + 2) = 0
log3x = −1 v log3x = −2
 jeszcze kilka przykladow i kolejny zestaw
jeszcze kilka przykladow i kolejny zestaw
 Dopiero od pazdziernika bede mogl sie calkowicie poswiecic matematyce.
Dopiero od pazdziernika bede mogl sie calkowicie poswiecic matematyce.  I moze tez troszke
innym zajeciom.
I moze tez troszke
innym zajeciom.
 ale też dobrze
D:
2x + 4x > 0 zawsze
ale też dobrze
D:
2x + 4x > 0 zawsze 


 http://www.wolframalpha.com/input/?i=log%5B10%2C+2%5Ex+%2B+4%5Ex%5D-log%5B10%2C+8%5D+%3D+log%5B10%2C+2%5E%28x-1%29+-+1%2F4%5D
http://www.wolframalpha.com/input/?i=log%5B10%2C+2%5Ex+%2B+4%5Ex%5D-log%5B10%2C+8%5D+%3D+log%5B10%2C+2%5E%28x-1%29+-+1%2F4%5D
