Wyznaczanie kąta znajc stasunki boków trójkąta Wojtek: Siema! Chciałbym wyznaczyć kąt α wiedząc, że cos(α)=−1/4 Pewnie jest to banalne, ale ja kończąc gimnazjum nie jestem w stanie jeszcze tego zrobić P.S. Jeśli użyłem złej funkcji to proszę o poprawkę

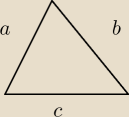
Wojtek: jeszcze podam boki trójkąta a=4 b=3 c=2 α kąt naprzeciwko boku a

Godzio:

	1
W takich przypadkach korzysta się z tablic trygonometrycznych cos(α) > 0 (więc −		chyba
	4

nie pasuje)

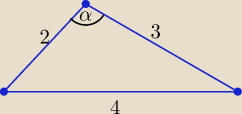
Bogdan: Dane są poprawne, trójkąt jest rozwartokątny, α > 90^o

Wojtek: to inaczej zadam to pytanie jak obliczyć kąt α (naprzeciwko boku a) znając długości wszystkich boków?

Bogdan: Można np.skorzystać z twierdzenia cosinusów. W tym przypadku:

	1
16 = 4 + 9 − 12cosα ⇒ cosα = −
	4

Założenie: 90^o < α < 180^o

	1
cosα = −		⇒ cosα ≈ −cos75o31' ⇒ cosα ≈ cos(180o − 75o31')
	4

α ≈ 104^o29'

Godzio: No tak, zasugerowałem się rysunkiem

Wojtek: skąd wartość −cos75^o 31' i skąd to założenie Założenie: 90^o < α < 180^o

Bogdan: Jeśli w trójkącie cosinus jednego z kątów jest ujemny, to miara tego kąta jest większa od 90^o i mniejsza od 180^o. Tutaj cosα = −0,25 < 0, więc α∊(90^o, 180^o). Dla cosα = 0,25 odczytujemy z tablic (można również wykorzystać kalkulator) α ≈ 75^o31', w konsekwencji jeśli cosα = −0,25, to cosα = −cos75^o31' i dalej cosα ≈ cos(180^o − 75^o31') ≈ cos104^o29'

Wojtek: dzięki, a czy mógłbyś mi jeszcze podać link do tablic lub sposób korzystania z kalkulatora? (CASIO fx−82ES)

Bogdan: Tablice sam poszukaj np. przez GOOGLE. Kalkulator: SHIFT → cos⁻¹0.25 = 1,318116072 (dla radianów) Przeliczamy teraz na stopnie i układamy proporcję: α = 1,318116072 180^o = π

	180o * 1,318116072
α =
	π

Kalkulator: 180x1,318116072 / SHIFT→π = 75.52248781 (uwaga: / to znak dzielenia) czyli 75.52248781^o 0,5225x60 = 31,35, czyli 31,35' ≈ 31 Ostatecznie otrzymujemy 75^o31' Można od razu ustawić kalkulator na stopnie

Wojtek: no bardzo podobnie mi wyszło (różnica sekundowa) dzięki za pomoc!

Bogdan: dlatego użyłem znaku ≈, można oczywiście zwiększyć dokładność obliczając wartość sekund.