1 sie 22:12
Mila:
A skąd masz te dane, sam wymyśliłeś?
Tam nie moga być takie kąty.
1 sie 22:22
matura: tak żeby sprawdzić poprawność tego wzoru
1 sie 22:23
Saizou : | | 1 | |
Mila ma rację przeliczyłem sobie i wyszedł mi cosα= |
| , co nie wskazuje na kąt 30o |
| | 5 | |
1 sie 22:24
Mila:
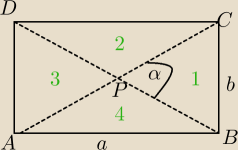
Wzór jest poprawny.
Dowód:
|AC|=d
| | 1 | |
1) Przekątne są równe i dzielą się na połowy; |PC|=|PB|= |
| d |
| | 2 | |
2)
P
Δ1=P
Δ2=P
Δ3=P
Δ4
| | 1 | | 1 | | 1 | | 1 | | 1 | |
PΔ1= |
| *|PC|*|PB|*sinα= |
| * |
| d* |
| d*sinα= |
| d2sinα |
| | 2 | | 2 | | 2 | | 2 | | 8 | |
1 sie 22:34
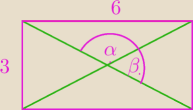
matura: a co do mojego rysunku jak wyznaczyć cosα ?
1 sie 22:36
max:
| | 2ab | |
sinα= |
| = ........... |
| | a2+b2 | |
1 sie 22:37
max:
| | 3 | |
@Saizou ........ cosα= |
| |
| | 5 | |
1 sie 22:41
matura:
a bo to nie jest trójkąt prostokątny ? więc tu nie ma tego a/c i tym podobne ?
1 sie 22:41
Saizou : | | 3 | |
tak cosα= |
| tak to jest jak się podniosło licznik do kwadratu  |
| | 5 | |
1 sie 22:44
max:
1 sie 22:46
matura: a może ktoś odpowiedzieć na pytanie post 22:41 ?
1 sie 22:48
Mila:
d=3√5
cosα:
62=(1,5√5)2+(1,5√5)2−2*1,5√5*1,5√5*cosα
Raczej oblicz cosβ:
32=(1,5√5)2+(1,5√5)2−2*1,5√5*1,5√5*cosβ
1 sie 22:49
Mila:
W ΔDPC liczymy cosα z tw. cosinusów.
1 sie 22:51
max:
| | 2ab | | 2*3*6 | | 4 | |
sinα= |
| = |
| = |
| |
| | d2 | | 45 | | 5 | |
| | 9 | | 3 | |
to cosα=+ √1−sin2α= √ |
| = |
| |
| | 25 | | 5 | |
1 sie 22:53
matura:
dziękuje za odpowiedź
1 sie 22:55
http://pl.wikipedia.org/wiki/Prostok%C4%85t