permutacje kicia16072: pomocy nie rozumiem ocb w tym zadaniu: Ile liczb pieciocyfrowych mozna utworzyc z cyfr 0,1,2,3,4 jesli cyfry nie moga sie powtarzac ? wiem ze wynik zadania to 96

67543: 4 na pierwszym miejscu − wstawiamy jedną z 4 cyfr bez 0 4 na drugim − ta, co na pierwszym, nie może być, ale 0 może 3 na trzecim − kolejna by się powtarzała (ta, co na drugim) 2 na czwartym − trzy z 5 by się powtórzyły (pierwsza, druga, trzecia) 1 na piątym (cztery poprzednie by się powtórzyły) 4*4*3*2*1 = 16*6= 32*3 = 96 (reg. mnożenia) Można też wykorzystać permutacje 5! −4! = 120 −24 = 96 Silnie oznaczają ilość ustawień 5 elementów w jednym rzędzie, ale odejmujemy 4!, gdyż to są ustawienia 4 elem. za zerem na początku... Trzeba przyznać że nie umiem tego tłumaczyć...

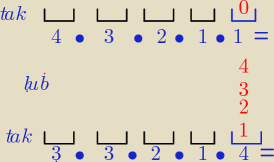
Eta: kropka na rys oznacza mnożenie po pierwsze ustawiasz zero na końcu tej liczby więc na piewszym miejscu masz 4 −− możliwości ustawień ( bo bez zera na drugim już tylko 3−y bo bez zera i bez tej pierwszej . itd... na zasadzie mnożenia otrzymasz: takich liczb: 4*3*2*1*1 = 24 drugi wariant , jeżeli na końcu ustawiasz liczbę różną od zera więc na poczatku masz 3−y możliwości ( bo bez tej ostatniej i bez zera , bo zero nie może być na pierwszym miejscu na drugim miejscu już może być zero , ale nie moze być ta ostatnia i ta pierwsza, więc masz też 3 możliwości na następnym już 2 mozliwości itd zatem ilość takich ustawień jest: 3*3*2*4 = ...... 4 możliwości na ostatnim miejscu dlatego ,że mogą tam być: 1, 2, 3, 4, zatem policz łącznie 4*3*2*1*1 + 3*3*2*1*4 = .......... i gotowe

kicia16072: ok dziekuje slicznie zrozumialam

Tomy: 0,1,2,3