Napisz równanie prostej przechodzącej przez punkty: wajdzik: Napisz równanie prostej przechodzącej przez punkty: A(5,−2) B(5,3)

	y2−y1
y−y1=		(x−x1)
	x2−x1

	3+2
y+2=		(x−5)
	5−5

	5x−25
y+2=
	0

y=−2 −> jak dla mnie to jest poprawne rozwiązanie. W książce jest wynik: "5" co mnie dziwi bo:

	5x−25
y+2=		//*0
	0

0=5x−25 x=5 To by świadczyło, że przemnożyli przez 0 a tak nie można. Z góry dziękuję za pomoc.

wmboczek: Lepiej korzystać ze wzoru bez ułamka − prosta nie musi być funkcją jak w tym przypadku (y−y1)(x2−x1)=(x−x1)(y2−y1)

wmboczek: no i wykonałeś dzielenie przez 0 a tak nie można

wajdzik: Teraz wyszedł dobry wynik, dzięki, będę się nim teraz obsługiwać.

Technik: 5a+b=−2 /(−1) 5a+b=3 −5a−b=2 5a+b=3 5

AS: Równanie w postaci wyznacznika | x − x1 y − y1 | | x2 − x1 y2 − y1 | = 0 np. Napisać równanie prostej przechodzącej przez punkty A(−1,−7) , B(2,2) | x + 1 y + 7 | | 2 + 1 2 + 7 | = 0 => 9*(x + 1) − 3*(y + 7) = 0 => 3*x − y − 4 = 0

wajdzik: Dzięki ale pozostanę przy tym co napisał wmboczek

5-latek: Przeciez tez niedawno pisalem CI to samo rownanie prostej w tej postaci a i tak wrociles do swojego Musisz zauwazyc ze rownanie prostej to nie tylko postac kierunkowa y=ax+b ale takze postac ogolna Ax+Bx+C=0 to co CI napisal AS a to przeciez jest proste bo dostaniesz wyznacznik 2 stopnia a ten przeciez potrafisz policzyc

	x		y
jest tez odcinkowa		+		=1 gdzie a i b nie rpwna sie zero
	a		b

i inne ale to poczytaj sobie Musisz to wiedziec bo nie zawsze jest lepiej korzystac z postaci kierunkowej

pigor: ... . Napisz równanie prostej przechodzącej przez punkty: A(5,−2) , B(5,3) . −−−−−−−−−−−−−−−−−−−−−−−−−−−− AB^→=[5−5,3+2]= [0.5] ⇔ n^→= [1,0] − wektor normalny szukanej prostej, więc np. 1(x−5)+0(y+2)=0 ⇔ x−5=0 − szukane równanie prostej . ...

wajdzik: 5−latek tak, po prostu gdzieś zgubiłem ten wzór i go już nie mogłem znaleźć. Ogólnie wkurzyłem się na pewien zbiór i teraz mam jeszcze inny i zaczynam wszystkie tematy z tego działu od nowa. Zadań sporo i robię kiedy mam czas. Pigor, postaram się w zadaniach ogarnąć wektory.

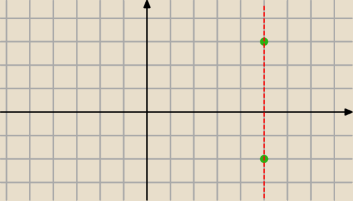
Mila: Wajdzik rysunek jest podstawą.