zaliczenie kasienka22: czesc wszystkim, mam na zaliczenie zrobic 4 zadania, a z matmy jestem noga. Pomocy! zad1 W graniastoslupie prostym prawidlowym szesciokatnym krawedz boczna ma dlugosc 6 cm, a przekatna scainy bocznej ma dlugosc12 cm a) wyznacz dlugosc krawedzi podstawy graniastoslupa b)wyznacz pole powierzchni calkowitej i objetosc graniastoslupa c)kat nachylenia przekatnej graniastoslupa do plaszczyzny podstawy zad2 W ostoslupie prawidlowym czworokatnym przekatna podstawy ma dlugosc 12cm, a wysokosc sciany bocznej ma dlugosc 3√7cm. wyznacz: a)dlugosc krawedzi podstawy b)wysokosc ostroslupa c) pole powierzchni calkowitej i objetosc ostroslupa zad3 W ostroslupie trojkatnym podstawa jest trojkatem prostokatnym rownoramiennym, w ktorym dlugosc przeciwprostokatnej jest rowna 12cm. Wszystkie krawedzie boczne ostroslupa sa rowne i maja dlugosc 12cm a)oblicz pole powierzchni calkowitej i objetosc ostroslupa b)wyznacz katy nachylenia krawedzi bocznych do plaszczyzny podstawy c)nachylenia sciany bocznej do plaszczyzny podstawy zad4 Wykaz, ze w prostopadloscianie suma kwadratow sinusow katków, pod jakimi jest nachylona jego przekatna do podstawy oraz dwoch sasiednich scian bocznych, jest rowna 1. Prosze o pomoc w miare możliwosci

asdf: w miare mozliwosci to podaj swoje obliczenia

kasienka22: nie wiem wogole jak mam sie do tego zabrac

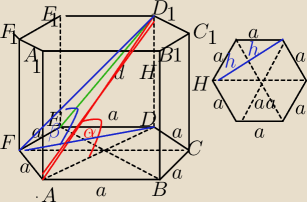Mila: Rozwiązuję zadanie 1.

Mila: Zadanie 1. H=6 cm d=12 cm a) W ΔEDD₁: d²=a²+H² 12²=a²+6² 144=a²+6² a²=108 a=√108=√36*3=6√3 b) P_c=2*P_6−kąta+6*a*H

	a2√3		(6√3)2√3
P6−kąta=6*		=6*		dokończ
	4		4

V=P_6−kąta*H podstaw i dokończ c) W ΔD₁AD: AD₁− najdłuższa przekątna graniastosłupa |AD|=2a=2*6√3=12√3

	DD1		6
tgα=		=
	AD		12√3

	1		√3
tgα=		=
	2√3		6

FD₁− krótsza przekątna gran. W ΔD₁FD:

	a√3
FD=2*		=a√3=6√3*√3=18
	2

	6		1
tgβ=		=
	18		3

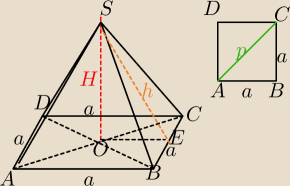Mila: Zadanie 2. p=12 cm h=3√7 a)dlugosc krawedzi podstawy W ΔABC: z tw. Pitagorasa p²=a²+a² 12²=2a²⇔144=2a² a²=72=P_□ABCD a=√72=√36*2=6√2 a=6√2 b)wysokosc ostroslupa

	1
|OE|=		a=3√2
	2

W ΔSOE: h²=H²+|OE|²⇔ (3√7)²=H²+(3√2)² 9*7=H²+9*2 dokończ c) pole powierzchni calkowitej i objetosc ostroslupa

	1
Pc=P□ABCD+4*		a*h
	2

podstaw i dokończ

Mila: Widzę, że to Cię wcale nie interesuje.

asdf: @Mila dlatego ja przestałem rozwiązywać zadania, do których nie ma własnych obliczeń

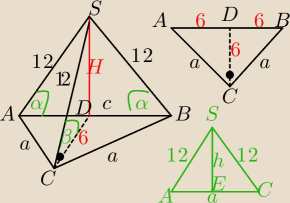Garth: Moze autor/ka zajrzy tutaj jeszcze jutro, mi np. zdarza sie zadac jakies pytanie i nie miec okazji sprawdzic odpowiedzi jeszcze tego samego dnia. Z kolei wydaje mi sie, ze najlepsza metoda edukacji jest, oczywiscie w zaleznosci od poziomu pytajacego, nasuwanie niewielkich wskazowek, tlumaczenie problemu.

Mila: Strategia zależy od tego , komu się pomaga. Zauważ, że zostawiłam część do samodzielnego dokończenia.

milla: interesuje mnie. Nie prosilabym o pomoc gdybym wiedziala jak to zrobic. Ale oczywiscie dokoncze zadania. Dzieki Mila

Mila: milla, trzeba jakoś reagować na rozwiązania, albo pytać, gdy masz wątpliwości, albo np. podziękować− wtedy wiadomo, że rozumiesz (ewentualnie analizujesz rozwiązanie). Co z dalszymi zadaniami, wiesz jak rozwiązać?

Mila: Zadanie 3. W ostroslupie trojkatnym podstawa jest trojkatem prostokatnym rownoramiennym, w ktorym dlugosc przeciwprostokatnej jest rowna 12cm. Wszystkie krawedzie boczne ostroslupa sa rowne i maja dlugosc 12cm. Rozw. Wszystkie krawędzie boczne są równe⇔spodek wysokości ostrosłupa leży w środku okręgu opisanego na podstawie⇔że leży w środku przeciwprostokątnej. a)oblicz pole powierzchni calkowitej i objetosc ostroslupa |AB|=c=12 cm 12²=a²+a² 144=2a²⇔a²=72 a=6√2

	1
|CD|=6 cm − promień okręgu opisanego na Δ prostokątnym jest równy		c
	2

W ΔCDS: 12²=6²+H² H=6√3

	1		1
PΔABC=		a2=		*72=36
	2		2

	1
V=		*36*6√3=... dokończ
	3

P_c=P_ΔABC+P_ΔABS+2*P_ΔACS WΔSEC: 12²=h²+(3p{2)² 144−18=h² h²=126 h=√126=√9*14=3√14

	1		1
PΔACS=		*a*h=		*6√2*3√14=... dokończ i oblicz Pc
	2		2

c) Kąty α=... napisz β=?

	CD		6		1
cosβ=		=		=
	CS		12		2

β=... napisz

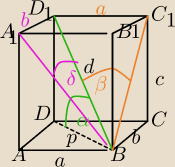Mila: Zadanie 4. Tu narysuję Ci te kąty w prostopadłościanie. Zadanie jest proste. α− kąt między przekątną d a płaszczyzną podstawy

	c
sinα=
	d

	a
sinβ=		w ΔD1C1B , kąt C1=90o
	d

	b
sinδ=		w ΔD1A1B
	d

Oblicz z tw. Pitagorasa p, potem d Podstaw do wzoru: sin²α+sin²β+sin²δ

milla: Mila bardzo mi pomoglas. Teraz sobie poradze Dziękuje jeszcze raz

Mila:

milla: Mila poglabys zrobic to konca 4 bo nie czaje

milla: albo ktos inny bo nie wiem tego

Mila: Zadanie 4. p=√a²+b² z tw. Pitagorasa w ΔABD w ΔD₁DB: d²=p²+c² d²=a²+b²+c²

	c2		c2
sin2α=		=
	d2		a2+b2+c2

	a2		a2
sin2β=		=
	d2		a2+b2+c2

	b2		b2
sin2δ=		=
	d2		a2+b2+c2

	c2		a2		b2
sin2α+sin2β+sin2δ=		+		+		=
	a2+b2+c2		a2+b2+c2		a2+b2+c2

	a2+b2+c2
=		=1
	a2+b2+c2

cnw