Przedstaw w układzie współrzędnych ilustrację zbioru A∩B wajdzik: Przedstaw w układzie współrzędnych ilustrację zbioru A∩B,gdy: A={(x,y):x²+y²+4x−6y+9=0}, B={(x,y):x²=y²} A: (x²+4x+4)+(y²−6y+9)=−9+9+4 (x+2)²+(y−3)²=2² Wiem, że ilustracja zbioru A∩B to liczby które są równocześnie w przedziale A i B. Ale nie wiem za bardzo jak się za to zabrać.

ICSP: x² = y² ⇒ |x| = |y| Rozpisuj teraz 4 przypadki

ICSP: albo : x² − y² = 0 ⇒ (x−y)(x+y) = 0 ⇒ y = −x v y = x Czyli to są dwie proste.

pigor: ..., a zbiór B: x²=y² ⇔ y²−x²=0 ⇔ (y−x)(y+x)=0 ⇔ y−x=0 lub y+x=0 ⇔ ⇔ y=x lub y= −x − graficznie suma dwóch prostych prostopadłych, przy czym tylko prosta y= −x ma część wspólną z A , czyli A∩B to 2 punkty − rozwiązania układu równań okręgu A i tej prostej . ...

pigor: ..., przepraszam . ...

wajdzik: z tego co widzę to za x możemy podstawić 1,2,3,4 i 5. To będzie iloczyn A i B?

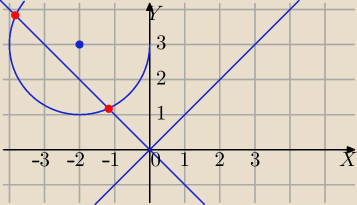
Mila: y=−x x²+y²+4x−6y+9=0 rozwiąż.

wajdzik: 2x²+10x+9=0 Δ=100−72 √Δ=2√7

	5+√7
x1=−
	2

	5−√7
x2=−
	2

wajdzik: Zgadza się

wajdzik: dzięki Milu

Mila: Za mało . Ma być zbiór punktów (x,y).

wajdzik:

	5+√7
y1=
	2

	5−√7
y2=
	2

Teraz powinno być ok, nie wiem gdzie ja mam głowę.

Mila: Dobrze obliczone. W takim razie tylko zostało wypisać pary : A∩B={(x₁,y₁)(x₂,y₂)}

wajdzik: jawohl!

pigor: ...,