ciagi
czarnaporzeczka: które wyrazy podanego ciągu są ujemne.
an=n2−9n+8
bn=2−3n
23 lip 20:53
Saizou : i w czym problem, obliczasz an<0 i bnn<0 + pamiętaj że n∊N+
23 lip 20:57
czarnaporzeczka: no nie umiem

naprawde

pomożesz?

23 lip 20:58
Krzysztof: Aby sprawdzić czy dany wyraz jest ujemny podstaw za n liczbę
23 lip 20:59
bezendu: a może chce gotowca

23 lip 20:59
czarnaporzeczka: mam poprawkę z matmy ... już ogarnełam wielomiany i funkcje a tych ciągów naprawde nie mogę
zrozrozumieć

23 lip 21:11
23 lip 21:12
czarnaporzeczka: to mam po prostu rozwiązać te równości tak po prostu i to bedzie koniec zadania ?
23 lip 21:19
Mila:
Rozwiąż nierówności:
a) n2−9n+8<0 i n∊N+
b) 2−3n<0 i n∊N+
Rozwiąż, to sprawdzę.
23 lip 21:19
czarnaporzeczka: a) delta=49
√delta=7
n=8 lub n=1
b) tu nie wiem

23 lip 21:24
Garth:
@Mila − czarnejporzeczce moze i uda sie rozwiazac te nierownosci, ale czy to zapewni mu/jej
zrozumienie tego zadania?
23 lip 21:28
czarnaporzeczka :
zadanie 1
n
2−9n+8<0
Δ=(−9)
2−4*8
Δ=81−32=49
√Δ=7
n∊{2,3,4,5,6,7} teraz dobrze ?
23 lip 21:32
Garth:
Ktore wyrazy podanego ciagu sa ujemne?
an = n2 − 9n + 8
Wiemy, ze ciag jest okreslony wzorem n2 − 9n + 8. Wiemy tez, ze ciag to funkcja, ktorej
argumentami sa liczby naturalne dodatnie, czyli przyjmuje wartosci [y na osi XOY, lub inaczej
ukladzie wspolrzednych] dla takich argumentow [x na osi XOY, lub inaczej ukladzie
wspolrzednych] jak 1, 2, 3, ... itd.
Te argumenty to nasze wyrazy, mamy wiec pierwszy, drugi, trzeci, ...itd. wyraz ciagu.
Np. wyraz drugi okreslimy tak: a2 = 22 − 9 * 2 + 8 [jak widac, po obu stronach rownania
podstawiamy 2 za n, 2, poniewaz to drugi wyraz ciagu.
Zeby zbadac, ktore wyrazy ciagu sa ujemne, badamy, dla jakich n funkcja ta przyjmie wartosc
ujemna, czyli n2 − 9n + 8 bedzie mniejsze od zera, co zapiszemy w jezyku matematyki wlasnie
ta nierownoscia, ktora podala Mila:
n2 − 9n + 8 < 0, no i pamietamy, ze n nalezy do liczb naturalnych dodatnich, czyli innymi
slowy n∊N+
23 lip 21:36
Mila:
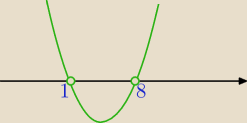
f(n)=n
2−9n+8 funkcja kwadratowa dla n∊R, jednak w ciągu interesują nas argumenty n∊N
+
n
2−9n+8=(n−1)*(n−8)
(n−1)(n−8)<0⇔n∊(1,8) i n∊N
+⇔
n∊{2,3,4,5,6,7}
ujemną wartość mają wyrazy
a
2,a
3,a
4,a
5,a
6,a
7 może sprawdź ( oblicz wg wzoru a
n=n
2−9n+8)
23 lip 21:37
Mila: No widzisz sam dobrze rozwiązałeś.
23 lip 21:38
Mila:

b
n=2−3
n
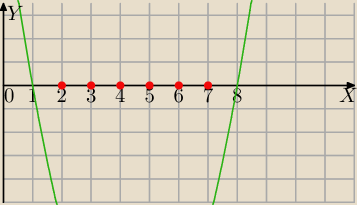
I sposób− narysujemy wykres funkcji
g(n)=2−3
n i n∊R
Interesują nas tylko wartości dla n∊N
+
Wszystkie wyrazy mają wartość ujemną
II sposób
2−3
n<0
2<3
n i n∊N
+
3
n>2 dla każdego n≥1 i n∊N
+
3
1=3 , 3>2
3
2=9>2
23 lip 21:50
 naprawde
naprawde  pomożesz?
pomożesz? 


 skoro opanowałaś wielomiany to nierówność
kwadratowa to nie problem więc do dzieła
skoro opanowałaś wielomiany to nierówność
kwadratowa to nie problem więc do dzieła 

 zadanie 1
n2−9n+8<0
Δ=(−9)2−4*8
Δ=81−32=49
√Δ=7
zadanie 1
n2−9n+8<0
Δ=(−9)2−4*8
Δ=81−32=49
√Δ=7
 f(n)=n2−9n+8 funkcja kwadratowa dla n∊R, jednak w ciągu interesują nas argumenty n∊N+
n2−9n+8=(n−1)*(n−8)
(n−1)(n−8)<0⇔n∊(1,8) i n∊N+⇔
n∊{2,3,4,5,6,7}
ujemną wartość mają wyrazy
a2,a3,a4,a5,a6,a7 może sprawdź ( oblicz wg wzoru an=n2−9n+8)
f(n)=n2−9n+8 funkcja kwadratowa dla n∊R, jednak w ciągu interesują nas argumenty n∊N+
n2−9n+8=(n−1)*(n−8)
(n−1)(n−8)<0⇔n∊(1,8) i n∊N+⇔
n∊{2,3,4,5,6,7}
ujemną wartość mają wyrazy
a2,a3,a4,a5,a6,a7 może sprawdź ( oblicz wg wzoru an=n2−9n+8)
 bn=2−3n
I sposób− narysujemy wykres funkcji
g(n)=2−3n i n∊R
Interesują nas tylko wartości dla n∊N+
Wszystkie wyrazy mają wartość ujemną
II sposób
2−3n<0
2<3n i n∊N+
3n>2 dla każdego n≥1 i n∊N+
31=3 , 3>2
32=9>2
bn=2−3n
I sposób− narysujemy wykres funkcji
g(n)=2−3n i n∊R
Interesują nas tylko wartości dla n∊N+
Wszystkie wyrazy mają wartość ujemną
II sposób
2−3n<0
2<3n i n∊N+
3n>2 dla każdego n≥1 i n∊N+
31=3 , 3>2
32=9>2