ciągi czarnaporzeczka: zad. 1 uczeń przygotowując się do egzaminu z matematyki rozwiązał 15 zadań i postanowił przez najbliższe 90 dni rozwiązywać po 5 zadań dziennie. Oblicz ile łącznie zadań rozwiąże o raz wyraź wzorem liczbę rozwiązywanych zadań w zaleźności od numeru kolejnego dnia pracy (oznacz ten nr przez n ) zad. 2 zbadaj monotoniczność podanych ciągów: a) an=1−(1/n) b) an= 1−2n−n² c) an=(−1/2)ⁿ dziękuje

pigor: ..., zad.1. Uczeń przygotowując się do egzaminu z matematyki rozwiązał 15 zadań i postanowił przez najbliższe 90 dni rozwiązywać po 5 zadań dziennie. Oblicz, ile łącznie zadań rozwiąże, oraz wyraź wzorem liczbę rozwiązywanych zadań w zależności od numeru kolejnego dnia pracy (oznacz ten nr przez n). −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− czy na pewno dobrze przepisała(e)ś treść zadania , bo niepokoi mnie słowo "rozwiązywanych'', wolałbym słowo "rozwiązanych" , a wtedy z warunków zadania − planu ucznia f(n)= 15+5n − wzór określający liczbę rozwiązanych zadań po n dniach ich rozwiązywania , stąd w n=90−tym dniu ich rozwiązywania f(90)= 15+5*90= 15+450= 465 − szukana liczba rozwiązanych zadań łącznie ...

Janek191: z.2

	1
a) an = 1 −
	n

więc

	1
an+1 = 1 −
	n+1

dlatego

	1		1		1		1
an+1 − an = [ 1 −		] − [ 1 −		] =		−		=
	n+1		n		n		n+1

	n + 1 − n		1
=		=		> 0 , bo n*( n + 1) > 0
	n*( n + 1)		n*(n + 1)

Ciąg ( a_n) jest rosnący. =====================

Janek191: z.2

	1
a) an = 1 −
	n

więc

	1
an+1 = 1 −
	n+1

dlatego

	1		1		1		1
an+1 − an = [ 1 −		] − [ 1 −		] =		−		=
	n+1		n		n		n+1

	n + 1 − n		1
=		=		> 0 , bo n*( n + 1) > 0
	n*( n + 1)		n*(n + 1)

Ciąg ( a_n) jest rosnący. =====================

Janek191: b) a_n = 1 − 2n − n² a_n+1 = 1 − 2*( n +1) − ( n +1)² = 1 − 2n − 2 − n² −2n − 1 = − 2 − 4n − n² więc a_n+1 − a_n = − 2 − 4n − n² − 1 + 2n + n² = −2n − 3 < 0 dla dowolnego n∊ N Ciąg jest malejący. c)

	1
an = (−		)n
	2

Jest to ciąg naprzemienny czyli niemonotoniczny.

	1
a1 = −
	2

	1
a2 =
	4

	−1
a3 =
	8

	1
a4 =
	16

...

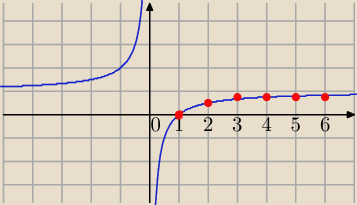
Mila: Zadanie 2. II sposób a) Możesz wykorzystać własności funkcji

	1
f(n)=1−		i n∊R, funkcja rosnąca w przedziale (0,∞)
	n

Nas interesują n∊N₊ ciąg jest rosnący,

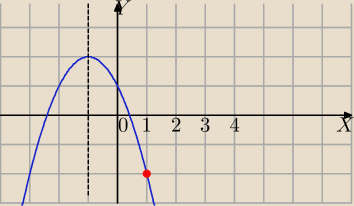
Mila: Zadanie 2. II sposób b) Możesz wykorzystać własności funkcji: f(n)=1−2n−n² dla n∊R f(n)=−n²−2n+1 szkicujemy wykres

	−b
xw=		=−1
	2a

y_w=2 funkcja jest malejąca dla x>0 Interesują nas n∊N₊, funkcja malejaca ciąg a_n=1−2n−n² jest malejący

pigor: ..., c) a_n=(−¹₂)ⁿ = (−1)ⁿ(¹₂)ⁿ i n∊N , więc dla n=2k − parzystych lub dla n=2k−1 − nieparzystych co się dzieje