Wyznacz długości krawędzi bryły oraz pole powierzchni całkowitej i objętość. brosky1: W graniastosłupie prostym prawidłowym trójkątnym suma długości wszystkich krawędzi jest równa 480 cm a przekątna ściany bocznej ma długość4√5 dm. Wyznacz długości krawędzi bryły oraz pole powierzchni całkowitej i objętość. Bardzo proszę o pomoc Ze stereometrii jestem kompletnie zielony

ICSP: a z twierdzenia Pitagorasa ?

brosky1: ja wogole nie wiem jak sie do tego zabrac

ICSP: ale twierdzenie Pitagorasa znasz Jak wrócę ze sklepu to zrobię

brosky1: dzieki wielkie

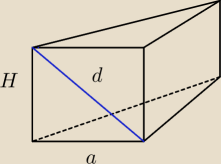ICSP: Z warunków : 1. Suma krawędzi = 480cm = 48dm 2. Przekątna ściany bocznej = 4√5 dm a mam obliczyć V oraz P_c i długości krawędzi (a oraz H) Oczywiście długość krawędzi musi być liczbą dodatnia zatem a > 0 oraz H > 0 Z twierdzenia Pitagorasa : a² + H² = d² ale d to przekątna ściany bocznej więc wiemy z 2. że d = 4√5 ⇒ d² = 80 mam pierwsze równanie : a² + H² = 80 Teraz zauważam ze graniastosłup prawidłowy trójkątny składa się z 9 krawędzi. Trzy na każdą podstawę oraz trzy boczne: 3a + 3a + 3H = 48 (z warunku 1.) 6a + 3H = 48 2a + H = 16 układ równań : 2a + H = 16 ⇒ H = 16 − 2a a² + H² = 80 a² + (16 − 2a)² = 80 a² + 256 − 64a + 4a² = 80

	44
5a2 − 64a + 176 = 0 ⇒ a = 4 v a =
	5

dla a = 4 mam H = 8

	44		88		80		88		8
dla a =		mam H = 16 − 2a = 16 −		=		−		= −		< 0 −
	5		5		5		5		5

sprzeczne z założeniem czyli zostaje przypadek a = 4 , H = 8 − długosci krawędzi policzone

	a2√3
V =		* H = 4√3 * 8 = 32√3
	4

	a2√3
PP =		+ 3aH = 8√3 + 96
	2