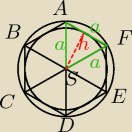
sześciokąt foremny Kasia16: Na sześciokącie foremnym opisano okrąg i w ten sześciokąt foremny wpisano okrąg. Pole powstałego pierścienia jest równe 2π dm². Oblicz pole powierzchni sześciokąta. zauważyłam, h to promień okręgu wpisanego = wysokość trójkąta równobocznego, czyli h = U{ a {3} }{ 2 } i dalej mam problem.. Bardzo proszę o pomoc .

Kasia16:

	a √3
h =
	2

Kasia16: proszę o pomoc

AROB: pomogę

Eta: dobrze zauważyłaś więc dalej tak: P_p = πR² − πr²

	a√3
R= a r=
	2

to: πR² − πr² = 2π => R² −r² = 2 podstaw dane i wyznacz ... a² bo: P_{sześciokąta} = 6*p_{Δrównoboczn.}

	a2√3
zatem; Psześciokąta = 6*
	4

Eta: Przepraszam AROB nie napisałam ,że pomagam...... obiecuję poprawę

AROB: Oznaczenia: P_sz − pole sześciokąta P_o − pole koła opisanego P_w − pole koła wpisanego P_p − pole pierścienia P_p = P_o − P_w P_o = πa²

	a√3		3a2
Pw = πh2 = π *(		)2 = π *
	2		4

Czyli po podstawieniu mamy:

	3
πa2 −		a2π = 2π /:π
	4

	3		1
a2 −		a2 = 2 ⇒		a2 = 2 ⇒ a2 = 8 ⇒ a = 2√2
	4		4

	a2*√3		3
Psz = 6 *		=		* 8√3 =12√3 [cm2]
	4		2

Eta: dodam swoje "3grosze" a² = 8 więc bez wyznaczania "a" można wyznaczyć pole ( będzie łatwiej

	8√3
Psz. = 6*		= 12√3 [cm2]
	4

AROB:

Kasia16: dziękuję

Rycho: jak obliczyć jeżeli znam tylko jeden wymiar promień sześcioboku który wynosi 80 centymetrów.Proszę o pomoc