. asdf: Witam, wytłumaczy mi ktoś przekształcenie w drugiej linijce? http://www.fotoszok.pl/upload/26edf409.png

pigor: o, nie, ja się brrr... boję tam wchodzić, aby nie dostać jakiegoś wirusoszoku

Mila: I słusznie, właśnie miesiąc temu "złapałam" kilka wirusów. Asdf zajrzałam. I po co Ci takie karkołomne przekształcenia, można to prosto zrobić.

asdf: @Mila jak? @pigor to zwykly uploader zdjec, pierwszy lepszy z google, Twoja sprawa, ze nie chcesz wchodzic, ale przegladarka tez jest uodporniona w pewnym stopniu od wirusów − ale jak wspomnialem − mi nic do tego P.S Od 3 lat nie instalowalem zadnego antywirusa, nie skanowalem zadnych plikow, a jak na razie komputer dziala i nie widze zadnych objawow wirusow.

Piotrek: to nie znaczy ze nic nie masz

Mila: Asdf zróżniczkuj obie strony równości: sin(arcsinx)=x

asdf: Dziękuje, ale chciałem to z definicji pochodnej wyprowadzić − zakładam na początku, że nie wiem ile to jest (arcsinx)'.

Trivial: asdf, tego się z definicji nie wyprowadza, bo jest trudno. Mamy równanie: sin(arcsinx) = x Różniczkując obustronnie (bez znajomości (arcsinx)'): cos(arcsinx)*(arcsinx)' = 1 Skąd:

	1
(arcsinx)' =
	cos(arcsinx)

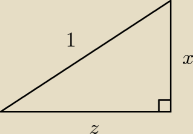
Teraz z zależności z rysunku:

	z
cos(arcsinx) =		= √1−x2.
	1

Czyli

	1
(arcsinx)' =		.
	√1−x2

Mila: Możesz też skorzystać tw. o pochodnej funkcji odwrotnej.

asdf: Próbowałem rozwiązać to z definicji, ale jak mówicie, że trudno to nie bede sie wysilac (odpoczywam ) Dziękuje raz jeszcze za pomoc, dobranoc

asdf: Próbowałem to rozwiązać z definicji, ale jak mówicie, że trudno to nie będę się wysilać (odpoczywam) Dziękuję raz jeszcze za pomoc, dobranoc