Wyprowadzenie wzoru na pole koła. fx: Hi, proszę o wskazówkę jak metodami licealnym wyprowadzić wzór na pole koła. Potrafię to zrobić całkując obwód okręgu w graniach [0, r] ale metodą licealną za bardzo nie mam pomysłu. Proszę o wskazówkę .

Trivial: Oblicz pole n−kąta foremnego i podąż z n do nieskończoności.

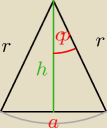
Trivial: Nasz n−kąt foremny dzielimy na n trójkątów jak na rysunku. Mamy dane r, n.

	1		2π		π
Zauważamy, że φ =		*		=
	2		n		n

Następnie:

	a/2
sinφ =		→ a = 2rsinφ
	r

	h
cosφ =		→ h = rcosφ
	r

	1		1		2π
P = n*|Δ| = r2*nsinφcosφ =		r2*nsin2φ =		r2*nsin
	2		2		n

	2π		2π
Teraz jedynie czego trzeba użyć, to przybliżenie sin		≈		i mamy wynik.
	n		n

	1		2π
P =		r2*n*		= πr2.
	2		n

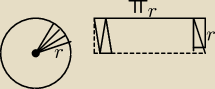
Mila: W LO wzór przyjmuje się do wiadomości. W GM : Rozcinamy koło jak na rysunku i układamy "prostokąt". P=πr*r=πr²

fx: Trivial − dziękuję . Proszę jednak na przyszłość o wskazówki a nie pełne rozwiązanie . Mila − przypomniałem sobie, że kiedyś się z tym sposobem spotkałem .

AS: Kiedyś w szkole podstawowej pokazano mi taki sposób. Koło o promieniu r podzielono na wycinki koła o małym kącie rozwarcia. Każdy wycinek potraktowano jako trójkąt o polu P1 = 1/2*c1*r Suma pól wszystkich wycinków wyniosła P = P1 + P2 + ... + Pn = 1/2*r*(c1 + c2 + ...+ cn) P = 1/2*r*2*π*r = π*r²