dd use: Mam pytanko jak policzyc przeciwdziedzine;

	√x2−4		3x−2
czegos takiego f(x)=		i takiego f(x)=√		− calosc pod pierwiastkiem
	x		x2−4

. chce to policzyc w taki sposob ze przyrównuje do a czyli;

	√x2−4
a=
	x

pokaze mi ktos jak to sie robi ^^ bede wdzieczny

pigor:

	√x2−4
... dobrze, niech a = ? wartość funkcji f danej wzorem f(x)=		,
	x

to (elementarnie − bez pochodnej) np. tak :

	√x2−4
a=		/*x i x2 ≥4 i x≠0 ⇒ ax= √x2−4 /2 i |x|>2 ⇔
	x

⇔ a²x²= x²−4 i D_f=(−∞;−2)U(2;+∞) ⇔ (a²−1)x²= −1, a taka równość (równanie) ma sens ⇔ a²−1<0 ⇔ |a|<1 ⇔ ⇔ a∊(−1;1) − szukana przeciwdziedzina danej funkcji f. ...

aniabb: np. zamieniasz x z y ..wyliczasz y i liczysz dziedzinę nowego czyli

	√y2−4
x=
	y

yx=√y²−4 y²x²=y²−4 y²(x²−1)=−4

	−4
y= √
	x2−1

D=R/{−1;1} i to jest przeciwdziedzina dla Twojego

use: a zrobicie mi jescze ten drugi przyklad bo jakos nie moge sie z nim uporac ....

use: >>>

pigor: ..., dziedzina tej funkcji, to niech będzie już twoją sprawą, wtedy

	3x−2		3x−2
a= √		⇒ a2=		⇔ a2(x2−4}= 3x−2 ⇔
	x2−4		x2−4

⇔ a²x²−3x+2−4a²= 0 i istnieje x∊D_f ⇔ (a=0 i x=²₃) lub (a≠0 i Δ ≥0) ⇒ ⇒ 9−4a²(2−4a²) ≥0 ⇔ 16a⁴− 8a²+9 ≥0 i ⇔ (4a²)²−2*4a²*1+1²+8 ≥0 ⇔ ⇔ (4a²−1)²+8 ≥ 0 dla a∊R , zatem (−∞;+∞) − szukana przeciwdziedzina . ...

use: to dlaczego wg wolframa http://www.wolframalpha.com/input/?i=sqrt%5B%283x-2%29%2F%28x%5E2-4%29%5D przeciwdziedzina to liczby rzeczywiste dodatnie ? jak to policzyc biorąc pod uwage dziedzine

	2
D=(−2,		>u(2,+oo)
	3

wiec jak tą dziedzine uwzglednic w tym rozwiązaniu zeby przeciwdziedzina wyszla prawidlowa tobie wyszla nieprawdziwa bo od (−oo,+oo)

pigor: ...kurcze no jasne , przecież jeśli zakładam a = f(x)= p(...) , to przecież muszę do swoich rozważań wziąć takie a ≥ 0 − z definicji pierwiastka kwadratowego i tyle musisz tylko jeszcze sprawdzić, czy na pewno x=²₃∊D_f jesli wolfram daje tylko a>0

use: wydaje mi sie ze dziedzina jest policzona dobrze , liczylem na kartce i nie wiedze błędu

use: wiec wkoncu jak to jest ; jezeli mam cos takiego ;

	3x−2
a=√		( pod pierwiastkiem ) i teraz jak podniose do kwadratu
	x2−4

	3x−2
a2=		to teraz ze wzgledu na to ze podnosilem do kwadratu biore zalozenie ze a>0
	x2−4

czy jak

use: a ... juz czaje ^^^ a jest pierwiastkiem kwadratowym , nie bylo tego posta wczesniejszego

use: dzieki stary juz kapuje ^^ zalezy mi na tym zeby takie prostsze przyklady potrafic rozwiązac bez ingerencji w analize matematyczną

pigor: ... zgadza się − wolfram pokazuje a nieujemne , a nie a dodatnie jak piszesz powyżej, więc w moim rozwiązaniu część wspólna a ≥0 i a=0 i a=R\{0} daje a ≥0, czyli D⁻¹= <0;+∞) − szukana przeciwdziedzina funkcji f. koniec, kropka . ...

Mila: No, poprawiliście, miałam pisać, że było błędnie (19:49) , ale ostatnio lękam się zwracać uwagę.

use: dlaczego sie lękasz zwracać uwage ? Przecież to forum matematyczne wiec wszystkim tutaj obecnym powinno zależec na tym żeby MATEMATYKA byla MATEMATYKĄ czyli była prawdziwa , a w przypadku kiedy ktos sie myli mysle ze nie mialby za zle zwrócenia uwagi na błąd bo wszystkim ( tak mysle ) zależy na tej prawdziwosci , zresztą co by nie mówic, to na tym forum, jedyne co nas wszystkich tutaj łączy to własnie matematyka więc pilnujmy jej poprawnosci ot co ^^

pigor: ... , h,mm, ... powiem szczerze nie rozumiem przedostatniego postu fioletowej pan−i(a)

use: jeszcze raz ja z pytaniem do tej przeciwdziedziny przykladowo ;

	3x−2
f(x)=3√		+x3
	x2−4

(tam jest pierwiastek 3 stopnia ) i szukam przykladowo przeciwdziedziny standardowo przyrównuje tak;

	3x−2
a=3√		+x3
	x2−4

czy moge teraz opuscic to +x³ i policzyc przykladowo

	3x−2
b=3√		i po policzeniu przeciwdziedziny b jakos dosjc do wyniku tej sumy?
	x2−4

bo licząc przyklad a=... wychodzi totalny kosmos po przeniesieniu x³ na drugą strone i podniesieniu do potegi 3 ^^

Basia: wykonaj klasyczne badanie przebiegu zmienności funkcji: liczenie granic konieczne; przeciwdziedzinę po zapisaniu wyników w tabelce i naszkicowaniu wykresu łatwo zapisać

Basia: P.S. czy x³ też jest pod pierwiastkiem ?

use: nie x³ nie jest pod pierwisatkiem

use: nie x³ nie jest pod pierwiastkiem , wlasnie chodzi o to ze te zadania musi sie dac rozwiązac bez badania przebiegu zmiennosci funkcji bo ten zakres wykraca poza ramy podrecznika

Basia: D = R\{−2;2}

	3x−2
g(x) =
	x2−4

	(3/x) − (2/x2)
limx→±∞ g(x) = limx→±∞		= 0
	1−(4/x2)

limx→−2− g(x) = −8*(+∞) = −∞ limx→−2+ g(x) = −8*(−∞) = +∞ limx→2− g(x) = 8*(−∞) = −∞ limx→2+ g(x) = 8*(+∞) = +∞ i w przedziałach (−∞;−2); (−2;2) ; (2;+∞) funkcja jest ciągła granice 3√g(x) będą takie same w efekcie mamy limx→−∞ 3√g(x)+x3 = 0 − ∞ = −∞ limx→−2− 3√g(x)+x3 = −∞ − 8 = −∞ limx→−2+ 3√g(x)+x3 = +∞ − 8 = +∞ limx→2− 3√g(x)+x3 = −∞+8 = −∞ limx→2+ 3√g(x)+x3 = +∞+8 = +∞ limx→+∞ 3√g(x)+x3 = 0 + ∞ = +∞ w przedziale (−∞; −2) funkcja ma zapewne jakieś maksimum a w przedziale (2;+∞) jakieś minimum ale możemy to zignorować bo w przedziale (−2;2) funkcja jest ciągła i przyjmuje wartości od −∞ do +∞ czyli przeciwdziedziną jest R posprawdzaj czy się gdzieś nie pomyliłam

zxcv: Mam retoryczne pytanie co wy liczycie przeciwdziedzinę czy zbiór wartości?

Basia: przeciwdziedzina = zbiór wartości

Basia: patrz: http://pl.wikipedia.org/wiki/Przeciwdziedzina

zxcv: To może spójrz na to: http://pl.wikipedia.org/wiki/Funkcja_%22na%22

zxcv: Według mojego rozeznania zbiór wartości jest podzbiorem przeciwdziedziny

Basia: A⊂A więc w jakimś sensie jest to prawda D⁻¹_f = {y: ∃_x∊D f(x) = y}

Basia: ad. 21:17 jest taka interpretacja, ale osobiście się z tym nie zgadzam na ogół piszemy sobie f:R → R tylko po to aby zaznaczyć, że funkcja przyjmuje wartości rzeczywiste, ale to wcale nie znaczy, że przeciwdziedziną jest cały zbiór R druga interpretacja jest taka: f(x) = x² jest funkcją z R w R, i funkcją z R na <0;+∞) jej przeciwdziedziną czyli obrazem dziedziny jest <0;+∞) i ja wolę tę a w tym zadaniu nie ma to znaczenia skoro obracamy się w obszarze funkcji rzeczywistych to przy tej pierwszej interpretacji mamy: ZW_f = R ⊂ D⁻¹_f ⇒ D⁻¹_f = R

zxcv: Dobrze a jak zaznaczyć dla f(x)= log x przeciw dziedzinę w przypadku gdy dziedziną jest N f: N → ? , nie wygodniej jest pisać f: N → R

use: Mam kolejny problem , jak policzyc przeciwdziedzine czegos takiego;

	1
f(x)=
	arcctg(x)−arctg(x)

dziedzina to oczywiscie x∊R\{1,−1} ale co z przeciwdziedziną

use: up up

use: up

aniabb: y∊(−∞;−2/π) u (2/π;∞)

use: wlasnie tez tak mi wyszlo , tylko ja to odczytalem z wykresu gdzie nanioslem obie funkcje , nie wiem za bardzo jak to obliczyc ( mialem wątpliwosci bo w odpowiedziach bylo cos takiego (−oo;−2/pi)u(2/3pi;+oo) ale to chyba jest ewidentny bląd w odpowiedziach). A jak to policzyc bez odczytywania z wykresu >?

Basia: lim_{x→ −∞} arcctg(x) = π

	π
limx→ −∞ arctg(x) = −
	2

	π		3π
limx→ −∞ arcctg(x) − arctg(x) = π − (−		) =
	2		2

	1		2
limx→ −∞		=
	arcctg(x) − arctg(x)		3π

lim_{x→ +∞} arcctg(x) = 0

	π
limx→ +∞ arctg(x) =
	2

	π		π
limx→ +∞ arcctg(x) − arctg(x) = 0 −		) = −
	2		2

	1		2
limx→ −∞		= −
	arcctg(x) − arctg(x)		π

nie ma błędu w odpowiedziach

	2		2
D−1 = (−∞; −		)∪(		;+∞)
	π		3π

oczywiście −∞ i +∞ wyjdą jak policzysz granice lewo i prawostronne w −1 i +1

Basia: @zxcv ad: wpis z 21:55 oczywiście, że wygodniej, ale to znaczy tylko tyle, że f jest funkcją określoną na N i mającą wartości w zbiorze R inaczej jest iniekcją z N w R nie znaczy natomiast, że cały R jest jej przeciwdziedziną

Basia: @use dziedziną nie jest R\{−1;1} tylko R\{1}

	3π		π
arcctg(−1) − atctg(−1) =		− (−		) = π
	4		4

use: hmm... w odpowiedziach tez tak jest ze D=R\{1} dlaczego wiec wolfram pokazuje ze roziwązanie rownania arccosx−arctgx=0 jest 1 i −1 hmmm ? http://www.wolframalpha.com/input/?i=arccotx-arctgx%3D0

use: juz chyba wiem na czym polega ta roznica ja narysowalem wykres arctg i arcctg miedzy tymi przerywanymi niebieskimi liniami ( arctg na czerwono a arc ctg na zielono , sklada sie z dwoch czesci ) a ty zapewene przyjelas ze arcctg to ten wykres zielono−różowy . Wiec wkoncu jaki jest prawidlowy

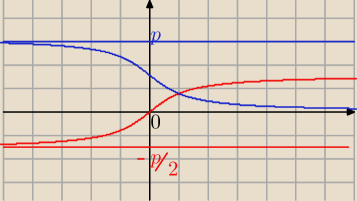
Basia: niebieskie arcctg(x) czerwone arctg(x)

Basia: i nie ma inaczej

use: no ale poczekaj bo to chyba jest kwestia tylko i WYŁĄĆĆZNIE umowy bo skoro arctg jest odwrotny do tg to moge sobie wziąść go na przedziale innym niż od −pi/2 do pi/2

use: To o co chodzi z wolframem ? dlaczego on liczy inaczej ?

Trivial: Już kilka razy mówiłem na forum, że wolfram ma inaczej zdefiniowany arcctg(x).

use: inaczej znaczy ze jednak to jest kwestia umowy

Trivial: Tak.

Basia: Tak, ale u nas taka umowa obowiązuje i tyle funkcja odwrotna do tgx z przedziału np. (^π₂; ^3π₂) to już nie jest arctg(x), tylko π+arctg(x) a z przedziału (−^3π₂; −^π₂) to −π+arctgx gdzie x nadal należy do (−π/2; π/2)

use: ok dzieki to juz wszystko jasne ^^

Basia: ostatnia linijka jest bez sensu; co innego chciałam napisać miało być: gdzie arctgx jest funkcją odwrotną do tgx z przedziału (−π/2;π/2)

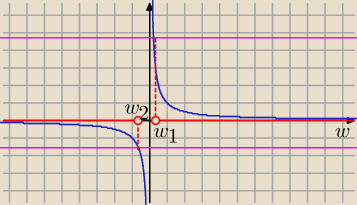
Mila: D=R\{1}

	π
arcctg(x)=		−arctg(x) [ spójrz na wykres Basi ]
	2

Niech w bedzie wartością funkcji:

1
	=w⇔
arcctg(x)−arctg(x)

1
	=w⇔
π   −2arctg(x) 2

2
	=w⇔
π−4arctg(x)

w*π−4w*arctg(x)=2 w*π−2=4w*arctg(x) /:(−4w ) i w≠0

2		πw
	−		=arctg(x)
4w		4w

−π		π		−π		1		π		π
	<arctg(x)<		stąd		<		−		<		⇔
2		2		2		2w		4		2

−π		1		π		1		π		π
	<		−		i		−		<
2		2w		4		2w		4		2

po rozwiązaniu:

	2		2
w<−		lub w>
	π		3π

Mila:

	1
Na wykresie funkcja y=
	w