trójkąt prostokątny gosia301: W trójkącie prostokątnym jeden z kątów ma miare 30stopni. Dwusieczna tego kąta dzieli przeciwległy bok o długości a na dwa odcinki. Wyznacz długości tych odcinków.

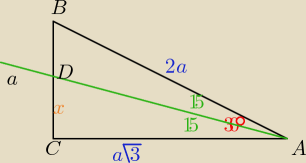
Janek191: Δ ABC − dany trójkąt D − punkt odcinka BC , taki, że I ∡ DAC I = 15^o α = I ∡ CBA I = 30^o I BC I = a I AC I = b I AB I = c

	a		1
sin α =		=		⇒ c = 2 a
	c		2

	√3		√3
b = c		= 2a		= a √3
	2		2

Niech x = I CD I, a − x = I DB I Mamy

	x		x
tg 15o =		=
	b		a√3

Ponieważ tg 15^o = 2 − √3 − z tablic lub można wyliczyć z wzoru na tg 2α więc

x
	= 2 − √3
a √3

x = ( 2 − √3)*a √3 = ( 2√3 − 3)*a oraz a − x = a − ( 2√3 a − 3a) = 4a − 2 √3a = ( 4 − 2√3)*a Odp. I CD I = ( 2√3 − 3)*a, I DB I = ( 4 − 2√3)*a ========================================

Janek191: Tam jest pomyłka. Powinno być α = I ∡ CAB I = 30^o I ∡ BCA I = 90^o

aniabb:

Janek191: QAniabb Dziękuję za rysunek Nie wiem jak się wpisuje liczby i litery

aniabb: naciskasz przycisk T a potem z klawiatury (cyfry tylko z górnego rzędu..numeryczna nie działa)

pigor: ..., lub z tw. o dwusiecznej kąta Δ np. tak :

x		a−x		x		a−x
	=		/*a ⇔		=		⇔ 2x= a√3−x√3 ⇔
a√3		2a		√3		2

⇔ (2+√3}x= a√3 /*(2−√3) ⇔ (4−3)x= a√3(2−√3) ⇔ x=|CD|= (2√3−3)a , zatem a−x= |BD|= a−a(2√3−3)= a(1−2p{3]+3)= a(4−2√3)=2(2−√3)a . ...