Napisz równanie okręgu symetrycznego do okręgu wajdzik: Napisz równanie okręgu symetrycznego do okręgu o równaniu: x²+y²−4x+6y−12=0 względem prostej y=3x+4

	1
y=−		x+b
	3

	7
b=
	3

	1		7
y=−		x+
	3		3

(x²−4x+4)+(y²+6y+9)=12+4+9 (x−2)²+(y+3)²=5² S(2,−3) r=5 {y=3x+4

	1		7
{y=−		x+
	3		3

	1		7
3x+4=−		x+		//*3
	3		3

9x+12=−x+7 10x=−5

	1
x=−
	2

	5
y=
	2

	1		5
P(−		;		)
	2		2

	x+2		x−3
O=(		;		)
	2		2

x=−3 y=2 Siedziałem trochę przy tym i cały czas mi wychodzi zły wynik.

	4		2
Odpowiedzi: (x+5		)2+(y+		)2=25
	5		5

Piotr: http://zadane.pl/zadanie/1243789 <<< Masz podobne tutaj zadanie , To zadanie numer 3

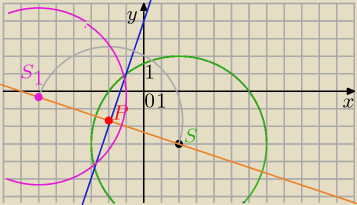Mila: x²+y²−4x+6y−12=0 ⇔(x−2)²+(y+3)²=25, S=(2,−3), r=5 względem prostej k: y=3x+4 Prostopadła do k

	−1		−1		1
m: y=		x+b i −3=		*2+b⇔b=−2
	3		3		3

	−1		7
m: y=		x−
	3		3

punkt przecięcia prostych k i m.

	−1		7
3x+4=		x−		/*3
	3		3

9x+12=−x−7 10x=−19 x=−1,9 y=3*(−1,9)+4=−1,7⇔P=(−1,9;−1,7)

	x+2		y−3
−1,9=		i −1,7=
	2		2

	−58		−29
x=−5,8=		=
	10		5

	−2
y=−0,4=
	5

	−29		−2
S1=(		,		)
	5		5

	29		2
(x+		)2+(y+		)2=25
	5		5

wajdzik: dzięki, przeanalizuje to.

wajdzik:

	7		7
Wszystko zrozumiałem, zrobiłem błąd rachunkowy. b=−		a nie		.
	3		3

Zbyt dużo mam tych błędów, nie wiem czy to te wakacje na mnie tak działają.

5-latek: Organizm sam daje CI do zrozumienia ze czas odpoczac .

wajdzik: Odpoczynek mam zaplanowany na przyszły rok gdy już napiszę matury.