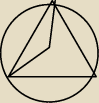
Oblicz pole trójkąta równobocznego wajdzik: Oblicz pole trójkąta równobocznego wpisanego w okrąg o równaniu: x²+y²+2x−7=0 −2x=2 −2y=0 x=−1 y=0 r=√x²+y²−z=√1+0+7=2√2 Jeżeli bok tego trójkąta równobocznego oznaczymy przez a , to ze wzoru na wysokość w trójkącie równobocznym będziemy mieć:

	2		a√3
2√2=r=		*
	3		2

	2		a√3
2√2=		*		//*6
	3		2

12√2=12√3a √2=√3a

	√2		√3		√6
a=		*		=
	√3		√3		3

	a2√3
P=
	4

	√6   ( )2*√3   3		6√3		1		√3
P=		=		*		=
	4		9		4		3

Czy wszystko jest ok

Saizou : no chyba jednak masz błąd rachunkowy

	2		a√3
2√2=		*
	3		2

	a√3
2√2=
	3

6√2=a√3

	6√2		6√6
a=		=		=2√6
	√3		3

wajdzik: tak, już poprawiam.

wajdzik:

	(2√6)2*√3		24√3
P=		=		=6√3
	4		4

Teraz powinno się zgadzać. dzięki wielkie