l fx: Wyznacz parametr m dla którego równanie x² + mx + 9 = 0 ma dwa pierwiastki mniejsze od −1. □ Δ > 0 ⇔ m² − 49 > 0 ⇔ (m − 7)(m + 7) > 0 ⇔ m ∊(−∞; −7) ∪ (7; +∞) □ x₁ < −1 ∧ x₂ < −1 Zadanie z działu wzory Viete'a a nie bardzo mam pomysł jak korzystając z tych wzorów to

	−b±√Δ
rozwiązać. Normalnie rozwiązując w wyznaczonej dziedzinie		< −1 to wiem jak
	2a

zrobić, ale nie widzę miejsca dla wzorów Viete'a. Pomożecie?

fx: Oczywiście Δ > 0 ⇔ m² − 36 > 0 ⇔ ...

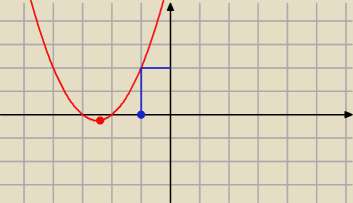
Basia: warunki konieczne i wystarczające: Δ>0

	−b
xw =		< −1
	2a

f(−1) > 0

Basia: P.S.1 można robić tak jak napisałeś, ale to dużo więcej liczenia P.S.2 też nie widzę miejsca dla wzorów Viete'a

fx: Ok, dziękuję za wskazówkę Basia . ...

	2
□ −		< −1 ⇔ −m < −2 ⇔ m > 2
	m

□ f(−1) > 0 ⇔ −m + 10 > 0 ⇔ m < 10 Uwzględniając powyższe warunki oraz dziedzinę m otrzymuję m ∊ (6; 10) Czy mogę prosić Basiu o jakieś podobne zadanko, albo dwa? Już kiedyś spotkałem się z podobną metodą ale o niej zapomniałem . Muszę przećwiczyć.

Basia: nie możesz mnożyć nierówności przez m, bo nie wiesz czy jest dodatnie czy ujemne

	−b		−m
poza tym xw =		=
	2a		2

−m
	< −1 /*2
2

−m < −2 /*(−1) m > 2 f(−1) dobrze

Basia: A już widzę..........dobrze zrobiłeś, a to chyba był tylko błąd w przepisywaniu

5-latek: Tylko ze w tym zadaniu powinna byc deita ≥0 (tak mi sie wydaje ) bo nie na napisane ze dwa rozne pierwiastki lub 2 pierwiastki dodatnie lub ujemne . jesli sie myle to prosze poprawic. To teraz masz np takie zadanie Dla jakich wartosci parametru m rownanie (m−1)x²−2mx+m−2 =0 ma dwa rozne ujemne pierwiastki rzeczywiste ?

Basia: Dla jakiej wartości parametru m równanie mx² − mx + 4 = 0 ma dwa pierwiastki rzeczywiste należące do przedziału: a) (−1;2) b) <−2;2> to trochę trudniejsze zadanie; musisz ustalić warunki dla m>0 i m<0 oddzielnie przypadek m=0 oczywiście odpada od razu, bo dla m=0 mamy równanie 4=0, które nie ma rozwiązania

fx: Dziękuję za zadania . 5−latek − dziękuję za zwrócenie uwagi na ten fakt . Muszę uważniej czytać zadania

Basia: @50−latek równanie st.2, w którym Δ=0 ma jeden pierwiastek podwójny

Basia: sorry; nie wiem skąd to 0

5-latek: Wlasnie w tym zadaniu ktore CI dalem do rozwiazania wykorzytaj wzoryVietea

fx: Zajmę się tym jutro bo dziś już pomęczyłem trochę logarytmów i przypomniałem sobie macierze i liczby zespolone .