s use: Mam podac odwzorowanie T ktore jest wyznaczone przez okreslone odwzorowanie plaszczyzny; i jest tak ; Symetria srodkowa wzgledem punktu (1,1) wg mnie to powinno wygladac tak; T(x;y)=(−x+1;−y+1) a w odpowiedziavch jest T(x;y)=(−x+2;−y+2) kto sie myli ja czy ksiązka

Basia: TY S(1,1) P(x,y) P'(x',y') SP^→ = −SP'^→ [x−1;y−1] = −[x'−1;y'−1] x−1 = −(x'−1) y−1 = −(y'−1) x−1 = −x'+1 y−1 = −y'+1 x' = −x+2 y' = −y+2

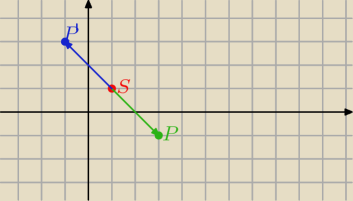
Basia: ilustracja do powyższego

Mila: Przekształcenie płaszczyzny,w którym obrazem dowolnego punktu P(x,y) jest taki punkt P'(x',y') że: x'=−x+2a y'=−y+2b jest symetrią środkowa względem punktu S=(a,b).

use: dzeki wielkie za proste i zrozumiale wytlumaczenie

use: A coś takiego jak będzie Podać przeciwobraz T⁻¹(MN) gdzie M=(0,2) N=(2;−4) T:(u,v)→(x,y) x=u y=2v moje rozumowanie jest takie ; T⁻¹(x,y)→(u,v)

	y
u=x v=
	2

i teraz tak jezeli MN to odcinek o koncach w punktach M=(0,2) i N=(2,−4) to kazdy punkt tego odcinka przeksztalca sie wedlug tego ; T⁻¹(x,y)→(u,v)

	y
gdzie u=x a v=
	2

czyli rezlutatem powinno chyba byc cos takiego ;

	2
T−1(MN) − odcinek o koncach w punktach (0,1) oraz (2,−2) [ bo M=(0,2) czyli M`=(0,		)
	2

	−4
oraz N=(2,−4) cxyzli N`=(2,		)]
	2

a w odpowiedziach jest (0,1) i (1,−2 ), nie czaje tego dlaczego 1 wyglada na to jakby 2 podzielil przez 2 ?

	y
a skoro punkt ma wspolrzedne P=(x,y) to wg tego ze u=x i v=		to tylko y powinien sie
	2

skracac przez 2, wyjasni mi to ktos ?

use: up

use: up up up

use: jest ktos w stanie mi pomóc?

Mila: Wydaje mi się, że masz rację. To przekształcenie to powinowactwo. Jeśli znajdę coś w literaturze, to napiszę potwierdzenie ( albo inne rozwiązanie). Napisz inne zadanie z tego tematu i odpowiedź.

use: ogolnie to całe zadanie brzmi tak ; Dane jest odwzorowanie T;R²→R² okreslone podanymi wzorami. a)podać interpretację geometryczną odwzorowania T b)podać odwzorowanie T⁻¹ c)podać obrazy T(AB) , T(K) gdzie A=(1,1) , B=(2,3) K=K(S,r) jest kołem o srodku S=(0,0) i promieniu r=6 d)Podac przeciwobraz T⁻¹(MN) gdzie M=(0,2), N=(2,−4) przykład 1.122. Tu,v)→(x,y) x=u , y=2v i odpiedzi sa takie ; ad a) Powinowactwo osiowe wzgledem osi OX o skali 2. ad b) T⁻¹(x,y)→(u,v) u=x v={y}{2}

	1
powinowactwo osiowe wzgledem osi OX o skali
	2

ad c) T(AB) − odcinek o koncach (1,2) i (2,6) T(K(0,0)6)− elipsa o polosiach a=6 i b=12 i srodku (0,0) ad d) T⁻¹(MN) −odcinek o koncach w punktach (0,1) i (1,−2) o ile odpowiedzi a,b,c sa dla mnie zrozumiale ( chociaz z okregiem troche dziwne ) to punkt d calkowicie mnie zmiażdzyl nie wiem dlaczego tam im wyszlo (1,−2) ....

use: Inny przyklad to np 1.123 jest taki; T: (u,v)→(x,y) x=3u y=v i teraz w tym przykladzie odpowiedz do podpunktu d jest taka ;

	2
ad d) odcinek o koncach (0,2) i (		, −4 )
	3

use: czyli tutaj tak jakby jest juz inaczej , podzielone jest tylko przez wspolrzednem x ( czyli tak jak podpowiada intuicja ) jednak chcialbym zeby ktos powiedział czy intuicja w tym przypadku jest ok czy nie bardzo i czy tamtem przyklad to zwyczajny irytujący blad w ksiazce ^^

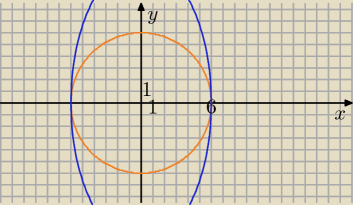
Mila: (Błąd w odp.) Wyjaśniam problem z elipsą. K: x²+y²=36 Przekształcenie przez powinowactwo względem OX w skali k=2 x'=x y'=2y x=x'

	1
y=		y'
	2

	y'2
x'2+		=36 /:36
	4

x'2		y'2
	+		=1⇔
36		144

x'2		y'2
	+		=1 opuszczamy znaczki '
62		122

x2		y2
	+		=1 równanie elipsy − postać kanoniczna
62		122

a=6 b=12

use: dzieki wielkie ^^

Mila: Zadanie dla USE określ przekształcenie w którym obrazem elipsy E jest okrąg K. E: 4x²+5y²=20 K: x²+y²=4 Podpowiedź: powinowactwo, napisz (odkryj) wzór: x'=... y'=...

use: ok. pomysle nad tym zadaniem Mam poza tym jeszcze jedno pytanie, rozwiązuje teraz zadania z funkcji, mam wyznaczyc naturalna dziedzine funkcji ( co nie jest problemem ) jednak poza tym mam wyznaczyc PRZECIWDZIEDZINE funkcji o podanym wzorze. Moje pytanie jest takie jaki jest sens w tego typu dzialaniu ? skoro gdzies przeczytalem ze ZW zbior wartosci nie zawsze pokrywa sie z przeciwdziedziną ( czasami tak) ale zazwyczaj ZW jest podzbiorem PRZECIWDZIEDZINY. Wiec teraz tak, jaki jest sens wyznaczania tej przecwidziedziny skoro z tego co ja rozumiem moze to byc nadzbior ZW czyli w szczegolnosci PRZECIWDZIEDZINA moze byc R ( zbior liczb rzeczywistych ). Może mi to ktos wyjasnic na czym ta roznica miedzy ZW a PRZECIWDZIEdZINĄ polega i po co ja wyznaczac skoro zawsze mozemy napisac ze przeciwdziedzina to R( prawdabo z tego co ja rozumiem to chyba tak )

Dominik: niech f: ℛ → ℛ, f(x) = x². zbiorem wartosci jest [0, ∞], natomiast przeciwdziedzina ℛ. natomiast dla g: ℛ → [0, ∞], g(x) = x², zbior wartosci funkcji g pokrywa sie z przeciwdziedzina i dlatego nazwiemy ja suriekcja. wyciagnij wnioski.

use: no dobra, wiec skoro mam funkcje okreslona wzorem ;

	√x2−4
f(x)=
	x

i nie mam okreslone czy funkcja jest R→R czy R²→R² to wychodzi na to że nie musze nic liczyc tylko napisze ze przeciwdziedzina jest R i odpowiedz jest poprawna..... to jest jakas paranoja ^^

Dominik: w tym momencie mowa zapewne o zbiorze wartosci.

use: odnosnie zadania podanego przez MILE ; K: x² +y²=4 E: 4x²+5y²=20 z elipsy trzeba uzyskac okrag zatem jezeli;

	4x2
E:		+y2=4 czyli
	5

	2x
E: (		)2+y2=4 wiec z tego zeby uzyskac okrag K
	√5

musimy zastosowac POWINOWACTWO OSIOWE WZGLEDEM OSI OY I SKALI U{√5{2}

use:

	√5
skala powinowactwa osiowego wzgledem osi oy
	2

mam nadzieje ze dobrze

Mila:

	2√5		2√5
x'=		x lub x'=−		x
	5		5

y'=y y'=y

use: ach... faktycznie mój błąd ,

	2		2
skala wyniesie		lub −
	√5		√5