całka IX: Wyznacz całke podwójną ∫∫D(10−5x−2y)dxdy Gdzie obszar D jest ograniczony linią x + |y| = 1 i osią OY

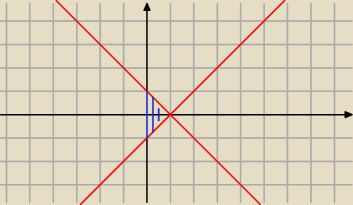
Basia: |y| = −x+1 ⇔ y = −x+1 ∨ −y = −x+1 ⇔ y = −x+1 ∨ y = x−1 Twój obszar D to obszar niebieski zastanów się jak zapisać granice całkowania po y i po x napisz co wymyśliłeś

TOmek: Dopiero co zacząłem ogarnianie całek podwójnych ale chyba tak będzie: D₁= 0≤x≤1 x−1 ≤y≤−x+1

Basia: dobrze czyli masz ₀∫¹dx _x−1∫^x+1(10−5x−2y) dy wiesz jak to policzyć ?

Basia: oczywiście górna granica to −x+1 (minus mi zjadło)

Basia: ∫(10−5x−2y)dy = 10y − 5xy − y² i mamy 10(−x+1)−5x(−x+1) − (−x+1)² − [ 10(x−1) − 5x(x−1) − (x−1)² ] = −10x+10+5x²−5x−(1−2x+x²) − [ 10x−10−5x²+5x −(x²−2x+1) ] = −15x+10+5x²−1+2x−x² − [ 15x−10−5x²−x²+2x−1 ] = 4x² − 13x + 9 − [ −6x² + 17x − 11 ] = 10x² − 20x + 20 czyli mamy ₀∫¹ (10x²−20x+20) dx =

	10
[		x2 − 10x2 + 20x ]01 =
	3

10		10		40
	− 10 + 20 − [ 0−0−0] =		+10 =
3		3		3