równanie damian: a²+b²=30 ab=5√5 Proszę o pomoc krok po kroku

ICSP: a = 5 b = √5 a = −5 b = −√5 a = √5 b = 5 a = −√5 b = −5 Metoda zgadywania zawsze najlepsza.

damian: a da się rozwiązać?

ICSP: Oczywiście że się da Oczywiście a ≠ 0 oraz b ≠ 0 nie spełniają tego układu nierówności. Zatem zakłądam rozwiązywanie dla a ∊ R\{0} , b∊R\{0}. Mogę wtedy bezpiecznie dzielić przez a² oraz b² gdyż bedą różne od 0 tak więc po podniesieniu II równania do kwadratu mam : a² + b² = 30 a²*b² = (5√5)² = 25 * 5 = 125 dzielę drugie równanie przez b² a² + b² = 30

	125
a2 =
	b2

Podstawiam do pierwszego

125
	+ b2 = 30 , przyjmuję t = b2 gdzie t > 0
b2

125
	+ t = 30
t

t² − 30t + 125 = 0 t₁ = ... ⇒ b₁ = ... , b₂ = ... ⇒ a₁ = ..., a₂ = ... t₂ = ... ⇒ b₃ = .... , b₄ = ... ⇒ a₃ = ... , a₄ = ... Równanie kwadratowe zakładam żę rozwiazać umiesz.

damian: straszne głupoty mi wychodzą z tego

AS: Oczywiście że się da. a² + b² = 30 , 2ab = 10√5 Stronami dodaje i następnie odejmuję a² + 2ab + b² = 30 + 10√5 a² − 2ab + b² = 30 − 10√5 (a + b)² = 30 + 10√5 (a − b)² = 30 − 10√5 a + b = √30 + 10√5 lub a + b = −√30 + 10√5 a − b = √30 − 10√5 lub a − b = −√30 − 10√5 stronami dodając i odejmując otrzymamy a i b. Rozważyć trzeba 4 przypadki (chyba)

ICSP: z czego ? z równania kwadratowego ?

damian: tak, t1=5 b=1 25^y=1 y=0 a to źle

AS: Uzupełniam − a i b muszą być tego samego znaku bo a*b > 0 , a więc mogą być tylko dwa rozwiązania a,b − dodatnie,bądż a,b − ujemne.

ICSP: t₁ = 5 t = b² b² = 5 ⇒ b₁ = √5 , b₂ = −√5 oraz a odpowiednio a₂ = 5 , a₂ = −5 drugi w identyczny sposób.

pigor: ..., a²+b²=30 i ab=5√5 ⇔ a²+b²=30 i 2ab= 2*5√5 /+ stronami ⇒ ⇒ (a+b)²=25+2*5√5+5 i ab=5p{5] ⇔ (a+b)²= (5+√5)² i ab=5p{5] ⇔ ⇔ |a+b|=5+√5 i ab=5√5 ⇔ (a+b=−(5+√5) i ab=5√5) lub (a+b=5+√5 i ab=5√5, stąd i ze wzorów Viete'a ⇔ (a,b)∊{(−5,−√5), (−√5,−5), (5,√5), (√5,5)} . ...

pigor: ...no właśnie tak ab= 5√5>0 , więc AS ma racje ±(a,b) . należy wywalic ,

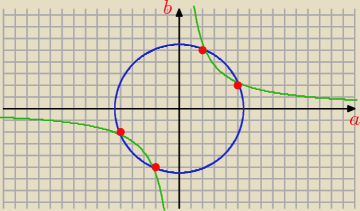
Bogdan: Dorzucam jeszcze jeden sposób rozwiązania i jego ilustrację. Weźmy prostokątny układ współrzędnych o osiach: oś odciętych a, oś rzędnych b.

	5√5
a2 + b2 = 30 jest okręgiem, ab = √125 ⇒ b =		jest hiperbolą.
	a

Widzimy, że krzywe przecinają się w czterech punktach, a więc układ równań ma 4 rozwiązania.

	5√5		125
b =		⇒ b2 =
	a		a2

	125
a2 + b2 = 30 ⇒ a2 +		= 30 /*a2
	a2

a⁴ − 30a² + 125 = 0 ⇒ a² − 30a² + 225 − 100 = 0 ⇒ (a² − 15)² − 10² = 0 (a² − 15 − 10)(a² − 15 + 10) = 0 ⇒ a² = 25 lub a² = 5 a = 5 i b = √5 lub a = −5 i b = −√5 lub a = √5 i b = 5 lub a = −√5 i b = −5

Damian: bogdan jak zawsze deklasuje wszystkich