3.22 zbiór pazdro 3 klasa Piotrek: 3.22 zbiór pazdro 3 klasa

	7
d) 0,4x+3+2,5−x−2<
	2

3.21

	√9
d) 3x/(x+2)>
	31/(x−1)

Piotrek: i jeszcze to 3^2x+2−2*3^x+2−27<0

Saizou :

	2		5		7
(		)x+3+(		)−x−2<
	5		2		2

2		2		2		7
	*(		)x+2+(		)x+2<
5		5		5		2

	2		2		7
(		)x+2(		+1)<
	5		5		2

	2		7		7		5
(		)x+2*		<		*
	5		5		2		7

	2		5
(		)x+2<
	5		2

2		2
	x+2<(		)−1
5		5

x+2>−x 2x>−2 x>−1 czy jakoś tak

Aga1.: 3^2x+2−2*3^x+2−27<0 (3^x)²*3²−2*3^x*3²−27<0 Wprowadź pomocniczą zmienną 3^x=t, t>0 i rozwiąż nierówność kwadratową.

pigor: ..., a ja lubię tak : D_r=R, a w niej mam ciąg nierównośći równoważnych : 3^2x+2−2*3^x+2−27< 0 /* 3⁻² ⇔ 3^2x−2*3^x−3< 0 , stąd i worów Viete'a ⇔ ⇔ (3^x+1)(3^x−3) <0 ⇔ 3^x−3< 0 ⇔ 3^x< 3⁰ ⇔ x<0, czyli x= R₋ = (−∞;0)

pigor: ..., lub 3.22d) 0,4^x+3+2,5^−x−2< ⁷₂ ⇔ (²₅)^x+3+(²₅)^x+2< ⁷₂ ⇔ ⇔ (²₅)^x+2 (²₅+1)< ⁷₂ ⇔ (²₅)^x+2* ⁷₅< ⁷₂ /* ⁵₇ ⇔ ⇔ (²₅)^x+2 < ⁵₂ ⇔ (²₅)^x+2 < (²₅)⁻¹ ⇔ x+2 > −1 ⇔ ⇔ x > −3 ⇔ x∊(−3;+∞) . ...

Saizou : oczywiście pigor ma racje nie wiem co zrobiłem że wpisałem −x poprawka: x+2>−1 x>−3

pigor: ..., otóż, dziedzina D_n= R−{−2,1} i w niej mamy ciąg nierówności równoważnych

	√9
3.21 d) 3x/ (x+2) >		/ *31/ (x−1) ⇔
	31/ (x−1)

⇔ 3^{x/ (x+2)}* 3^{1/ (x−1)} > 3 ⇔ 3^{x/ (x+2)+1/ (x−1)} > 3¹ ⇔

	x		1		x(x−1)+1(x+2)−(x+2)(x−1)
⇔		+		> 1 ⇔		> 0 ⇔
	x+2		x−1		(x+2)(x−1)

	x2−x+2−x2−x+2		−2x+4
⇔		> 0 ⇔		> 0 ⇔
	(x+2)(x−1)		(x+2)(x−1)

⇔ −2(x−2)(x+2)(x−1) > 0 ⇔ x<−2 lub 1< x < 2 ⇔ x∊(−∞;−1)U(1;2) . ...

Piotrek: do pierwszego odpowiedz powinna byc (−3,+∞)

Piotrek: pomylilo mi sie odpowiedz do drugiego sie nie zgadza, ma byc (−∞,−2) suma (1,4)

Eta:

	3
2/ 3x/x+2>		założenie x≠−2 i x≠1
	31/(x−1)

	x		1		x		x		x−2
		> 1−		⇔		> {x−1−1}{x−1} ⇔		−		>0
	x+2		x−1		x+2		x+2		x−1

	x2−x−x2+4		4−x
		>0 ⇔		>0
	(x+2)(x−1)		(x+2)(x−1)

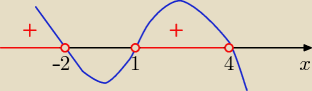
równoważna postać iloczynowa i rys. ( od dołu z prawej strony przez miejsca zerowe miejsca zerowe x= −2 v x= 1 v x= 4 (4−x)(x+2)(x−1)>0 ⇔ x€ (−∞, −2) U (1,4)

pigor: , to mogłeś poszukać sobie błędów w moim rozwiązaniu, bo ja widzę je (tylko błędy mojej nieuwagi − dwa) w dwóch ostatnich linijkach pierwszy w liczniku nierówności "zjadłem" x, wtedy byłoby w liczniku −x+4, a nie jak jest −2x+4, a drugi w ostatniej linijce jest x<−2, a ja piszę x∊(−∞;−1) nie wiem dlaczego i tyle

Eta:

pigor: ..., dziękuję Eta , a swoją drogą Twój sposób rozwiązania jest o niebo lepszy od mojego ... niestety .

piotrek: pigor gdybym znalazł to bym się głupio nie pytał. Moje rozwiązanie było identyczne jak ety tylko zamiast √9 wpisalem 3^0,5, sprawdzałem z 10 razy ani razu nie zauważyłem

pigor: , no i dobra , tak trzymaj