

 rozwiązując układ równań prostych;
y = 3x +4 i x +2y −1 =0
otrzymasz: A( −1, 1)
punkt P( 2,3) jest środkiem odcinka AC
więc C( xC, yC)
to: xC= 2xP− xA i yC = 2yP −yA
podstawiając odowiednie współrzędne otrzymasz:
xC= 5 i yC= 5 to C(5,5)
Wyznaczamy równanie prostej DC II do pr.AB i zawierającej punkt C
zatem: pr. DC: y − yC = a( x −xC)
gdzie a = 3 , bo to wsółczynnik kierunkowy prostej AB: y = 3x +4
zatem: po podstawieniu danych otrzymasz:
pr.DC: y= 3x −10
rozwiązując układ równań prostej DC i prostej AD
czyli: y= 3x −10 i x +2y −1=0
otrzymasz współrzędne punktu D( 3,−1)
więc współrzedne punktu B wyznaczyysz:
xB = 2xP − xD i yB= 2yP − yD
otrzymasz: B( 1, 7)
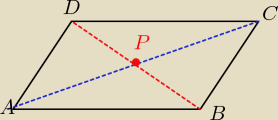
zaznacz teraz te punkty w układzie współrzędnych, przekonasz się ,że
czworokąt ABCD jest własnie tym równoległobokiem.
Drugie zad. może rozwiąże ktoś inny ( bo już nie mam siły)
Idę na herbatkę
rozwiązując układ równań prostych;
y = 3x +4 i x +2y −1 =0
otrzymasz: A( −1, 1)
punkt P( 2,3) jest środkiem odcinka AC
więc C( xC, yC)
to: xC= 2xP− xA i yC = 2yP −yA
podstawiając odowiednie współrzędne otrzymasz:
xC= 5 i yC= 5 to C(5,5)
Wyznaczamy równanie prostej DC II do pr.AB i zawierającej punkt C
zatem: pr. DC: y − yC = a( x −xC)
gdzie a = 3 , bo to wsółczynnik kierunkowy prostej AB: y = 3x +4
zatem: po podstawieniu danych otrzymasz:
pr.DC: y= 3x −10
rozwiązując układ równań prostej DC i prostej AD
czyli: y= 3x −10 i x +2y −1=0
otrzymasz współrzędne punktu D( 3,−1)
więc współrzedne punktu B wyznaczyysz:
xB = 2xP − xD i yB= 2yP − yD
otrzymasz: B( 1, 7)
zaznacz teraz te punkty w układzie współrzędnych, przekonasz się ,że
czworokąt ABCD jest własnie tym równoległobokiem.
Drugie zad. może rozwiąże ktoś inny ( bo już nie mam siły)
Idę na herbatkę
 , dzięki AROB
właśnie piję herbatkę i pojadam chałwę
, dzięki AROB
właśnie piję herbatkę i pojadam chałwę 
 Zad. 2. Należy najpierw sprawdzić,które boki trójkąta prostokątnego zawierają się w danych
prostych.
I prosta: y = 2x + 3, II prosta: x + y − 12 = 0 ⇒ y = −x + 12
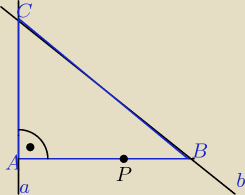
Nie są to proste prostopadłe, więc jedna prosta zawiera jedną z przyprostokątnych, a druga
przeciwprostokątną. ( patrz rysunek).
− Wyznaczamy współrzędne punktu C, jako punktu przecięcia prostych a i b, czyli rozwiązujemy
układ równań: y = 2x + 3
y = −x + 12 ⇒ 2x − 3 = −x + 12 ⇒ x = 5
Wtedy y = −5 + 12 = 7, Zatem punkt mamy:
C(5,7)
−Wyznaczamy równanie prostej AB prostopadłej do prostej a i przechodzącej przez punkt P(2,1).
Wykorzystujemy warunek prostopadłości prostych.
Zad. 2. Należy najpierw sprawdzić,które boki trójkąta prostokątnego zawierają się w danych
prostych.
I prosta: y = 2x + 3, II prosta: x + y − 12 = 0 ⇒ y = −x + 12
Nie są to proste prostopadłe, więc jedna prosta zawiera jedną z przyprostokątnych, a druga
przeciwprostokątną. ( patrz rysunek).
− Wyznaczamy współrzędne punktu C, jako punktu przecięcia prostych a i b, czyli rozwiązujemy
układ równań: y = 2x + 3
y = −x + 12 ⇒ 2x − 3 = −x + 12 ⇒ x = 5
Wtedy y = −5 + 12 = 7, Zatem punkt mamy:
C(5,7)
−Wyznaczamy równanie prostej AB prostopadłej do prostej a i przechodzącej przez punkt P(2,1).
Wykorzystujemy warunek prostopadłości prostych.
| 1 | 1 | |||
ma = 2, mAB = − | = − | |||
| ma | 2 |
| 1 | 1 | |||
y − 1 = − | (x−2) ⇒ y=− | x+2 −−−−−− prosta AB | ||
| 2 | 2 |
| 1 | ||
y = − | x + 2 | |
| 2 |
| 1 | 5 | 2 | ||||
y = 2x + 3 ⇒ 2x + 3 = − | x + 2 ⇒ | x = −1 ⇒ x = − | . | |||
| 2 | 2 | 5 |
| 2 | 1 | 2 | 1 | |||||
Wtedy y = 2*(− | ) + 3 = 2 | . Zatem mamy punkt A(− | , 2 | ) | ||||
| 5 | 5 | 5 | 5 |
| 1 | 1 | |||
y = − | x + 2 ⇒ −x + 12 = − | x + 2 ⇒ x = 20 | ||
| 2 | 2 |
| 2 | 1 | |||
Odp. A(− | , 2 | ), B(20, −8), C(5,7) | ||
| 5 | 5 |





 przydało mi się
przydało mi się