n fx: (k + 1)x² + 2x + 1 = 0 dla jakiej wartości k równanie ma dwa pierwiastki o przeciwnych znakach? założenia: □ k ≠ −1 □ Δ > 0 ⇔ 4 − 4k − 4 > 0 ⇔ −4k > 0 ⇔k < 0

	2
□ x1*z2 < 0 ⇔		< 0 ⇔ k< −1
	k+1

Uwzględniając te trzy warunki otrzymuję rozwiązanie k ⊂ (−∞; −1). Pytanie: kiedy jako rozwiązanie podaje się sumę a kiedy część wspólną zbiorów? Czy dobrze rozumiem, że mając < otrzymuję część wspólną a kiedy > − sumę?

ZKS: Niestety nie. Podam przykład −x² + 1 > 0 i czy tutaj mamy sumę x ∊ (−∞ ; −1) ∪ (1 ; ∞) czy raczej część wspólną x ∊ (−1 ; 1)? Mam nadzieję że o to właśnie się pytałeś.

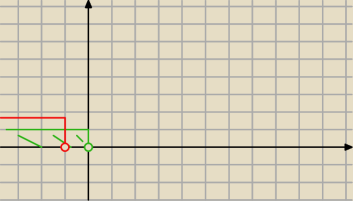
fx: Mam na myśli coś innego. Tj. jakby szereg warunków liniowych. Jak je interpretować. Przykład w 1. poście. Rysunek − skąd mam wiedzieć, że rozwiązanie problemu z 1. postu to Cz ∩ Zie a nie Cz ∪ Zie.?

fx: Ok, już rozumiem. Przecież nie może być jednoczenie k < −1 ∧ k > −1.

ZKS: Dokładnie o to chodzi że ten parametr musi spełniać te wszystkie warunki zatem bierzemy część wspólną.

fx: To samo równanie ale teraz do ustalenia są wartości m aby rozwiazania były nieujemne. Rozpatruję dwa przypadki: a) Δ > 0 ⇔ m ∊ (−∞; −1) ∪ (5; +∞)

	5
x1x2 = 0 ⇔ m = −
	4

x₁+x₂ > 0 ⇔ m < 0

	5
Jaka jest część wspólna? −
	4

b) Δ > 0 ⇔ m ∊ (−∞; −1) ∪ (5; +∞)

	5
x1x2 > 0 ⇔ m > −
	4

x₁+x₂ > 0 ⇔ m < 0

	5
część wspólna (−		; −1)
	4

Więc na podstawie a i b otrzmuję, że m ∊ [−5/4; −1). Czy dobrze mam tę część wspólną w a?

fx: Nie to równanie . Równanie, które rozpatrywałem w poście z 00:25 ma postać: x² + mx + m+5/4 = 0

ZKS: A jak jest napisane rozwiązania czy różne rozwiązania?

fx: Dla jakich wartości m równanie ma dwa różne nieujemne pierwiastki.

ZKS: I to jest ważne że dwa różne ponieważ wtedy rozpatrujemy Δ > 0.

fx: To wiem, stąd rozpatruję ten warunek

ZKS: Mogłeś od razu dać warunki Δ > 0 ∧ x₁x₂ ≥ 0 ∧ x₁ + x₂ ≥ 0.

ZKS: Ale na początku napisałeś rozwiązania dlatego dopytywałem ponieważ liczyłeś Δ > 0.

ZKS: Oczywiście x₁ + x₂ > 0.