ciagi zadanie: wykaz, ze ciag jest ograniczony z gory a_n=4+3n²−n⁴

asdf: skoro z gory to jest malejący: lim_n→∞ a_n = −∞ i juz.

asdf: skoro z gory to jest malejący: lim_n→∞ a_n = −∞ i juz.

zadanie: to wystarczy?

zadanie: ?

zadanie: czy to bedzie wystarczajace?

Trivial: asdf, na pewno nie znasz żadnych ciągów rosnących ograniczonych z góry?

asdf: @Trivial znam, ale ten ciąg na pewno tak nie ma, więc od razu dałem odpowiedź − jaka praca wlasna taka odpowiedź...

Basia: @asdf ciąg ograniczony z góry wcale nie musi być malejący (ten jest, ale Ty piszesz tak jakby to była prawda ogólna, a nie jest) przykłady:

	(−1)n
an =
	n

	n−1
bn =
	n

Basia: @zadanie będzie wystarczające, jeżeli potrafisz udowodnić takie twierdzenie: lim_n→+∞ a_n = −∞ ⇒ a_n jest ograniczony z góry a to łatwo udowodnić

zadanie: dziekuje a moglbym prosic o udowodnienie bo jednak nie potrafie

asdf: @Basia nie pisze, ze kazdy − odwołałem sie jedynie do tego ciągu.

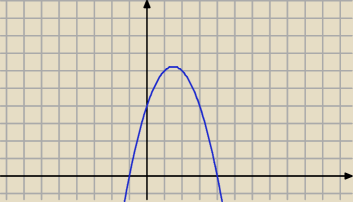
Mila: an=4+3n²−n⁴ Zbiór wartości funkcji: f(x)=−x⁴+3x²+4 x²=t f(t)=−t²+3t+4 i t≥0 Δ=9+16=25

	−3−5		−3+5
t1=		=4 lub t2=		=−1
	−2		−2

	−3		3
tw=		=
	−2		2

	3		3
yw=−(		)2+3*		+4
	2		2

	−9		9		1		3
yw=		+		+4=6		największa wartość f(x) dla x=		>0
	4		2		4		2

	1
Zwf={−∞,6		)
	4

Dokończ .

Trivial: asdf, "skoro z góry, to jest malejący" trudno zrozumieć jako odwołanie do tego konkretnego przykładu.

Basia: lim_n→+∞ a_n = −∞ ⇔_def. ∀_N<0 ∃_n0∊N ∀_n>n0 a_n<N stąd wynika, że np. dla N= −1 ∃_n0∊N ∀_n>n0 a_n<−1 a stąd mamy ∀_n∊N a_n ≤ S=max{−1; a₁,a₂,....,a_n0} czyli ciąg jest ograniczony z góry bo S jest liczbą skończoną

Basia: P.S. jeżeli to jest szkolne zadanie, to lepiej zastosuj rozwiązanie, które przedstawiła Mila

zadanie: dziekuje bardzo

asdf: ale sie czepiacie..

Basia: nie czepiamy się asdf; wymagamy ścisłości, dla Twojego własnego dobra

asdf: napisalem, ze ∞ ma wartosc −∞, wiec sie tyczylo tego ciagu, ale nie ma co przeciągac, wskazowka na przyszlosc mi sie przyda