Trygonomietria Nie umiem: Zbadaj, czy funkcja jest okresowa, jesli tak, zbadaj jej okres. f(x) = sinx + cosx f(−x) = −sinx + cos x No i tutaj mam problem. Wydaje mi sie, ze funkcja nie jest ani parzysta, ani nieparzysta, natomiast odpowiedz do tego zadania wskazuje co innego.

	π
No bo wezmy np. argument		.
	4

	π
f(		) = √2
	4

	π
f(−		) = 0
	4

ZKS:

	1		1
sin(x) + cos(x) = √2[		sin(x) +		cos(x)] =
	√2		√2

	π		π		π
√2(sin(x)cos(		) + sin(		)cos(x)] = √2sin(x +		)
	4		4		4

Nie umiem: Czyli:

	π
f(x) = √2sin(x+		)
	4

	π
f(−x) = − √2sin(x+		)
	4

stad funkcja ta jest parzysta, zgadza sie? No i nie rozumiem tez, skad sie bierze takie, a nie inne wyrazenie po drugim znaku rownosci w Twoim dzialaniu.

ZKS: Aby funkcja była parzysta co musi być spełnione? Co do Twojego pytania to myślałem że wiesz o tym

1		π		π
	= sin(		) = cos(		).
√2		4		4

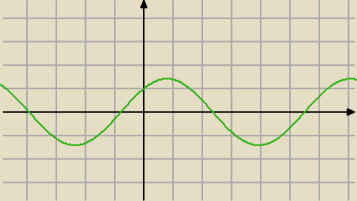
Mila: f(x)=sinx+cosx Czy parzysta? f(−x)=sin(−x)+cos(−x)=−sinx+cosx ≠f(x) i f(−x)≠−sinx−cosx nie jest ani parzysta ani nieparzysta Z definicji okresowości funkcji: f(x+T)=f(x) T jest niezależne od x, T>0 sin(x+T)+cos(x+T)=sinx+cosx Albo skorzystaj z postaci od ZKS

Nie umiem:

Nie umiem:

Nie umiem: Aby funkcja byla parzysta, wartosci argumentow musza byc takie same, jak ich przeciwne odpowiedniki. Zboczylismy jednak troche z tematu, bo w zadaniu chodzi o okresowosc Funkcja jest okresowa, poniewaz jej wykres jest przeksztalceniem funkcji sinx, jednakze tu jej wartosci sa pomnozone przez √2, a takze przesuniete o pi/4 w lewo, zgadza sie?

Nie umiem: I tak, jednak nie jest parzysta. Przepraszam takze, za moje nietypowe puste odp. ale pisze z tel. i jesli ktos mnie tu uprzedzi z odp., kiedy ja jestem w trakcie pisania, to dzieja sie dziwne rzeczy

Mila: Ze wzoru :

	π
f(x)=√2sin(x+		)
	4

wniosek T=2π 1) sinx jest funkcją okresową o okresie zasadniczym 2π Współczynnik √2 'wydłuża" wykres− nie zmienia okresu

	π
2) +		przesuwa wykres sinx w lewo− nie zmienia okresu⇒
	4

T=2π

PW: A tak w ogóle to najpierw pytałeś o okresowość, a potem bardzo się martwisz o parzystość. To są zupełnie różne pojęcia, czy przypadkiem ich nie utożsamiasz w jakiś sposób? Funkcja f(x)=x², x∊R jest parzysta, ale ni ma nic wspólnego z okresowością. Parzystość to inaczej symetria wykresu względem prostej x=0. Wykres funkcji parzystej f(x)=cosx po przesunięciu równolegle do osi OX o wektor [a,0] staje się symetryczny względem prostej x=a (ale parzystość może się "popsuć").