ciagi
zadanie: | | n+2 | |
jak obliczyc granice tego ciagu: an=(−1)n |
| ? |
| | 3n−7 | |
7 lip 16:43
zadanie: | | (−1)n(n+2) | | | |
lim |
| =lim |
| dobrze? |
| | 3n−7 | | | |
7 lip 17:02
Mila:
Granica nie istnieje.
(−1)n ciąg ograniczony naprzemienny
Gdyby była sytuacja:
an=(−1)n *cn, gdzie cn→0 to granica 0.
7 lip 17:08
zadanie: dziekuje
7 lip 17:10
zadanie: a czy ten ciag bedzie ciagiem ograniczonym?
7 lip 17:11
zadanie: ?
7 lip 17:20
Mila: Tak.
7 lip 17:39
zadanie: bo w ksiazce mam napisane ze ograniczeniem tego ciagu jest np. A=5 dlaczego akurat 5 ? anie 3
czy 4?
7 lip 17:45
zadanie: mowie o tym ciagu poczatkowym (tym co nie ma granicy)
7 lip 17:47
zadanie: moglbym prosic o pomoc
7 lip 18:03
Mila:
Funkcja homograficzna :
| | x+2 | |
f(x)= |
| jest malejąca przedziałami. |
| | 3x−7 | |
nas interesują x∊N
+
obliczamy a
1, a
2
| | n+2 | |
cn= |
| ciąg malejący począwszy od n≥3 |
| | 3n−7 | |
A=5 jest ograniczeniem na wyrost. ( sprawdź rachunki)
7 lip 18:20
zadanie: ale tam jest jeszcze (−1)n
7 lip 18:24
7 lip 18:29
Mila:
Tak, liczysz a
n, ja rozważyłam ciąg c
n, a wartości ciągu a
n będą oscylować.
Możesz osobno rozważyć wyrazy dla n nieparzystych i n parzystych.
| 3 | | −5 | | 6 | | −7 | |
| ,−4, |
| , |
| , |
| ,... |
| 4 | | 2 | | 5 | | 8 | |
7 lip 18:34
zadanie: dziekuje
7 lip 18:47
zadanie: mam jeszcze kilka pytan
7 lip 18:47
zadanie: | | 3n+2 | | 5 | |
ciag an= |
| moze byc ograniczony z dolu np. przez |
| a z gory np. przez 3? |
| | n+7 | | 8 | |
7 lip 18:49
Mila:
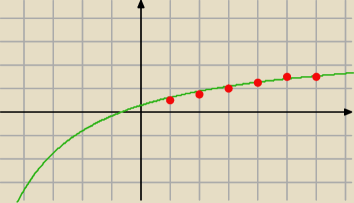
Tak.
a
n ciąg rosnący, a
n>0
Lim
n→∞a
n=3
a
n ograniczony z góry 3.
3n+2<3(n+7)
2<21 prawda dla n∊N
+
7 lip 19:02
zadanie: ok dziekuje
wykaz, ze ciag(an) jest ograniczony z dolu
an=n−102003
ciag jest ograniczony z dolu jesli an≥m czyli
n−102003≥m
m≤n−102003 dla n=1 mam:
m≤1−102003 mozna tak wykazac ? (jesli nie to sa moze jakies inne sposoby?)
7 lip 19:08
Mila: Dobrze.
an jest ciągiem rosnącym
dla n=1 ma wartość najmniejszą
n−102003≥1−102003 co jest oczywiste
W poprzednim zadaniu, też dodaj komentarz, że dla n=1 ma wartość najmniejszą.
7 lip 19:32
zadanie: ok dziekuje
| | n+1 | |
zbadaj ograniczonosc ciagu (an)= |
| |
| | n | |
| | n+1 | | 1 | |
an= |
| =1+ |
| dla n=1 mam: |
| | n | | n | |
z nierownosci −2≤a
n≤2 dla n∊N
+ wynika, ze ciag a
n jest ograniczony. a to jest dobrze?
7 lip 19:39
zadanie: ?
7 lip 19:52
Mila:
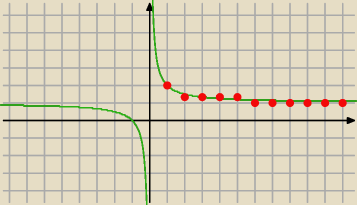
Tak.
a
n>0
a
1=2 największa wartość
a
n>1 i a
n≤2
7 lip 21:17
zadanie: dziekuje bardzo
wroce jeszcze do przykladu z 19:32
jest to ciag rosnacy wiec aby wykazac, ze jest on ograniczony z dolu mozna by udowodnic, ze
jest on rosnacy(an+1−an>0) i posluzyc sie na stwierdzenie, ze kazdy ciag rosnacy jest
ograniczony z dolu?
7 lip 22:17
Mila:
Tak.
f(x)=x−102003 funkcja liniowa rosnąca, zatem
f(n)=n−102003 funkcja rosnąca dla n∊N+
Korzystaj z własności znanych funkcji, ale z definicji też będzie dobrze, lecz więcej pracy.
7 lip 22:25
zadanie: dziekuje
7 lip 22:29
zadanie: a jak wykazac, ze ciag an=2n−n2 jest ograniczony z dolu? bo jak robilem tym sposobem co
wczesniej to mi nie wychodzilo
7 lip 23:15
Mila:
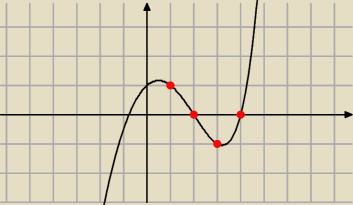
To nie jest ciąg monotoniczny,
zbadaj kiedy maleje, kiedy rośnie, znajdź najmniejszą wartość.
7 lip 23:29
zadanie: Najmniejsza wartosc to −1 bo, a3=8−9, czyli jest ograniczony z dolu przez −1 tak?
7 lip 23:43
Mila: Tak.
7 lip 23:54
 Tak.
an ciąg rosnący, an>0
Tak.
an ciąg rosnący, an>0
 Tak.
Tak.
 To nie jest ciąg monotoniczny,
zbadaj kiedy maleje, kiedy rośnie, znajdź najmniejszą wartość.
To nie jest ciąg monotoniczny,
zbadaj kiedy maleje, kiedy rośnie, znajdź najmniejszą wartość.