ciagi zadanie: mam pytanie: czy kazdy ciag rosnacy jest ograniczony z dolu a kazdy ciag malejacy jest ograniczony z gory?

Trivial: Tak. Dzieje się tak dlatego, że wartości ciągu zaczynają się od pewnego n − np. od n=0 albo n=1. Załóżmy że wartości zaczynają się od n=0. Wtedy mamy: 1. Dla ciągu rosnącego zachodzi a_n−1 < a_n. Rozwijając to dalej otrzymujemy: a₀ < a₁ < a₂ < ... < a_n (dla dowolnego n) Zatem ciąg a_n jest ograniczony z dołu. 2. Dla ciągu malejącego analogicznie. (a_n−1 > a_n) Co innego jeśli chodzi o funkcje. Dla funkcji nie jest to prawda (weź np. funkcję f(x) = x).

zadanie: dziekuje

zadanie: to jeszcze zapytam: kiedy ciag nie jest ograniczony? wedlug mnie wtedy gdy jest ograniczony tylko z dolu lub tylko z gory lub ani z dolu ani z gory dobrze?

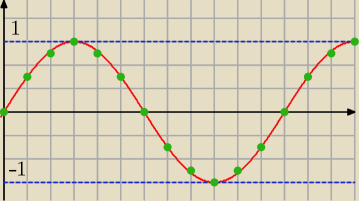
Trivial: Tak. Ciąg ograniczony to taki, którego wszystkie wartości mieszczą pomiędzy dwoma

	π
liczbami. Np. ciąg an = sin(n*		) jest ograniczony. Wszystkie jego wartości mieszczą się
	6

pomiędzy liczbami −1 i 1 (−1 ≤ a_n ≤ 1).

zadanie: dziekuje