Zbiór liczb, których odległość na osi liczbowe od liczby -2 jest równa 4, można kamczatka: Zbiór liczb, których odległość na osi liczbowe od liczby −2 jest równa 4, można opisać równaniem: Odpowiedź: |x+2| = 4 Ale czy mógłby mi ktoś to rozrysować graficznie ?

use: normalnie w ten sposob ; https://matematykaszkolna.pl/strona/1097.html

5-latek: jesli masz takie rownanie |x+2|=4 to graficzne rozwiazujesz go tak . Rysujesz os liczbiowa i na osi zaznaczaz liczbe przeciwna do liczby ktora masz w module czyli u nas bedzie to −2 . Teraz przesuwasz sie o 4 w leweo i zazznaczasz i tak samo o 4 w prawo i zaznaczasz ile to bedzie . Algebraicznie rozwiazujesz to tak |x+2|=4 x+2=4 i x+2=−4 rozwiaz te rownania i sprawdz czywyniki wyszly te same .

bezendu: 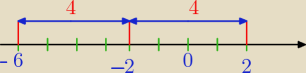5−latek mały błąd nie będzie tak ''i'' tylko ''lub'' x+2=4 lub x+2=−4 x=2 lub x=−6 @kamczata masz graficznie tak jak chciałeś

5-latek: masz racje pomylka z rozpedu bo rowiazywalem co innego jeszce .

bezendu: każdemu się może zdarzyć