Jeżeli liczba a należy do przedziału (−8;−4), to wyrażenie I −a−2 I można zapis kamczatka: Jeżeli liczba a należy do przedziału (−8;−4), to wyrażenie |−a−2| można zapisać w postaci: a) −a−2 b) a−2 c) −a+2 d) a+2 Odp to A. Znalazłem tutaj na forum to zadanie ale dalej nie kumam. Wybieram np. z przedziału liczbę −3 podstawiam i wychodzi |−5| = 5 , więc według odp A : −5 − 2 = −7 o to chodzi ?

Basia: a∊ (−8;−4) ⇔ −8 < a < −4 /*(−1) ⇔ 8 > −a > 4 / −2 ⇔ 6 > −a−2 > 2 skoro −a−2 > 2 to jest dodatnie czyli −a−2>0 ⇒ |−a−2| = −a−2

Basia: albo graficznie; narysuję Ci

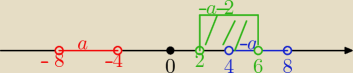Basia: −a symetria względem 0 −a−2 przesuwasz o 2 w lewo no i widać teraz, że −a−2 > 0

kamczatka: już wiem o co chodzi dzięki za tak ibszerne wytłumaczenie zadania.

kamczatka: Wracam jeszcze do tego zadania bo pasuje mi tu rowniez odpowiedz −a+2 , bo co tutaj nie podstawie z przedzialu to wychodzi mi liczba dodatnia, to czemu odpowiedz ta jest zla?

5-latek: Kolego . Przeciez znany definicje wartosci bezwzglednej |x|=x dla x≥0 czyli opuszczajac wartosc bezwzgledna nie mieniamy znaku na przeciwny . ale jest takze |x|=−x dla x<0 czyli opuszczajac wartosc bezwzdgledna zmieniamy znak na przeciwny Teraz juz wiesz ze dla tego przedzialu czyli a∊(−8.−4) to co jest w srodku tego modulu jest dodatnie to popatrz na definicje ktrora mowi nam ze opuszczajac wartosc bezwzgledna (modul ) nie zmieniamy znaku czyli |−a−2|=−a−2 i i to jest prawidlowa odpowiedz do tego zadania . . A co by bylo gdybysmy musieli opuscic modul ze zmiana znaku na przeciwny . Wtedy by to wygladalo tak |−a−2|=−(−a−2)=a+2. tak by bylo gdyby to co w srodku w module wyszlo ujemne .