DANY JEST CIĄG O WYRAZIE OGÓLNYM KARPYK: Dany jest ciąg o wyrazie ogólnym a_n = − n² +8n +2 a) określ monotoniczność ciągu (a_n ) b) czy ciąg ten jest ograniczony ? c) czy ciąg ten ma wartość najmniejszą i największą ?

Trivial: a_n = −n² + 8n + 2 = −(n² − 8n − 2) = −[(n−4)²−16 −2] = 18 − (n−4)². Spróbuj teraz.

KARPYK: −[(n−4)²−16 −2] = 18 − (n−4)² nie rozumiem skąd to się wzięło.

KARPYK: (n−4)² = n² + 8n +8 , a dalej nie rozumiem toku myślenia

bezendu: a_n+1=−(n+1)²+8(n+1)+2=−(n²+2n+1)+8n+8+2=−n²−2n−1+8n+10=−n²+6n+9 a_n+1−a_n=−n²+6n+9−(−n²+8n+2)=−n²+6n+9+n²−8n−2=−2n+7

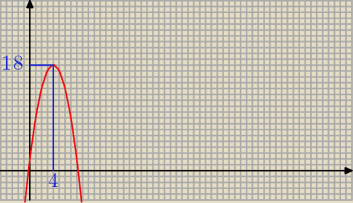
Trivial: Z mojej postaci można od razu odczytać, że mamy parabolę o ramionach skierowanych w dół i wierzchołku w punkcie (4,18). Skąd od razu: 1. Ciąg a_n osiąga wartość największą (równą 18) w punkcie n = 4. 2. Ciąg a_n (n∊N) rośnie na przedziale n∊(−∞,4), a maleje na przedziale n∊(4,∞)

Trivial: KARPYK, po prostu przekształciłem do postaci kanonicznej (kombinując wzorami skróconego mnożenia)

KARPYK: postać kanoniczna to 4 lata wstecz dla mnie bo na studiach jestem ,ale przypomnę sobie , mam 2 sposoby rozwiązania więc myślę , że dam radę , dziękuję i pozdrawiam