| ez | ||
Obliczyć ∫L | dz, gdzie L jest okręgiem o równaniu |z−i|=1. | |
| (1+z2)2 |
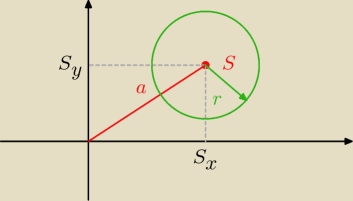 |z−a| = r to zwykłe równanie okręgu ukryte w zapisie zespolonym.
Niech z = x + iy oraz a = Sx + iSy, a także S = (Sx, Sy). Mamy:
|z−a| = |x+iy − Sx − iSy| = |x−Sx + i(y−Sy)| = √(x−Sx)2 + (y−Sy)2 = r /2
(x−Sx)2 + (y−Sy)2 = r2
|z−a| = r to zwykłe równanie okręgu ukryte w zapisie zespolonym.
Niech z = x + iy oraz a = Sx + iSy, a także S = (Sx, Sy). Mamy:
|z−a| = |x+iy − Sx − iSy| = |x−Sx + i(y−Sy)| = √(x−Sx)2 + (y−Sy)2 = r /2
(x−Sx)2 + (y−Sy)2 = r2
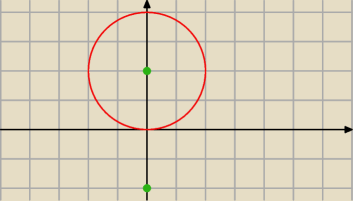 A do tego zadania: pierwiastkami są z1,2 = i oraz z3,4 = −i. Wybieramy punkt i.
A do tego zadania: pierwiastkami są z1,2 = i oraz z3,4 = −i. Wybieramy punkt i.
| ez | 1 | d | ez | ||||
resz=i[ | ] = limz→i | [(z−i)2 | ] | ||||
| (1+z2)2 | 1! | dz | (1+z2)2 |
| d | ez | ez(z+i)2 − 2ez(z+i) | ||||
= limz→i | [ | ] = limz→i | ||||
| dz | (z+i)2 | (z+i)4 |
| −4 − 4i | 1+i | |||
= ei | = −ei | |||
| 16 | 4 |
| ez | 1+i | πi | ||||
∫L | dz = 2πi*(−ei | ) = − | (1+i)ei.// można sobie wymnożyć | |||
| (1+z2)2 | 4 | 2 |