:/
ICSP: Dwa zadania dla
Przyszłych maturzystów 
1. Znajdź takie m aby nierówność była spełniona dla każdego x ∊ R :
| | x2 + mx − 2 | |
−3 < |
| < 2 |
| | x2 − x + 1 | |
2. Nierówność :
3 lip 16:46
Piotr: Ja spróbuje pozniej zrobic, bardzo ciekawe zadania

3 lip 17:04
Piotr: Zadanie 1
Założenie
x2−x+1≠0
Δ<0
D=R
1. −3x2+3x−3<x+mx−2
−4x2+x(3−m)−1<0
Δ<0
Δ=9−6m+m2−16=m2−6m−7<0
Δ'=36+28=64<0
m1=7 ; m2=−1
m∊(−1;7)
2. x2+mx−2<2x−2x+2
x2−2x−mx+4>0
x2+x(−2−m)+4>0
Δ<0
Δ=(−2−m)−4=m2+4m=m(m+4)<0
tutaj okrelsam miejsce zerowe m=0 ; m=−4
m∊(−4,0)
Cześć wspolna 1 i 2 to przedzial m∊(−1;0)
3 lip 17:16
Janek191:
1) Mianownik jest dodatni , więc można pomnożyć przez x2 − x + 1
3 lip 17:18
Piotr: W zadaniu 2 wyszedł mi koncowy wynik x∊(−∞,1)
3 lip 17:40
ICSP: Pierwsze prawie dobrze. W drugim wynik zły.
3 lip 17:56
ICSP: policz jeszcze raz deltę w nierównośći : x2 − (m + 2)x + 4 > 0
Polecam wzór a2 − b2 w tej delcie.
3 lip 18:03
Piotr: Widze juz blad nie pomnozylem przez ''4'' zaraz poprawie
3 lip 18:05
Piotr: x+x(−2−m)+4>0
Δ<0
Δ=(2−m)−42=(2−m−4)(2−m+4)<0
2−m−4=0 2−m+4=0
m=−2 ; m=6
m∊(−2;6)
Czesc wspolna 1 i 2 to przedzial m∊(−1,6)
3 lip 18:08
Piotr: Zle jeszcze raz:
Δ=(−2−m)2−42=(−2−m−4)(−2−m+4)<0
m=−6 ; m=2
m∊(−6;2)
Czesc wspolna 1 i 2 to przedzial m∊(−1;2)
3 lip 18:15
ICSP: pierwsze dobrze.
Zostąło jeszcze drugie.
3 lip 19:00
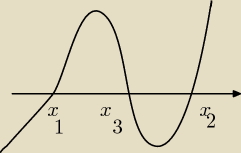
Saizou :
zał:
2−5
x≠0
5
x≠2
x≠log
52
x∊R\{log
52}
(2−5
x)(−5
2x+2*5
x+15)<0
−1(2−5
x)(5
x−5)(5
x+3)<0
x
1=log
52 x
2=log
55 x
3=log
53
no i rysujemy 'wężyka' od góry pamiętając że log
52 nie ma w dziedzinie
x∊(−
∞:log
52) ∪ (log
53:1)
3 lip 19:14
ZKS:
Saizou chyba coś nie teges lepiej to popraw.
3 lip 19:20
Saizou : właśnie coś mi tu nie pasuje, tak to jest jak się liczy od razu na komputerze

3 lip 19:21
ZKS:
Czy 5x + 3 może być równe 0?
3 lip 19:23
Piotr: Ja to probowalem robić wprowdzilem zmienna pomocnicza t i w sumie wszystko ladnie wychodzilo,
ladne liczby ale zla odpowiedz ; /. Tutaj z logarytmem cos zwiazane musi byc

?. Ja to
pomnozylem przez kwadrat mianownika, potem wprowdzilem za 5
x=t ale i tak lipa ; /. Sprobuje
pozniej

3 lip 19:24
ZKS:
Jeżeli robisz podstawienie 5x = t to to t jakie jest?
3 lip 19:25
asdf:
t = 5x, t ≠ 2:
(t−2)(t2−2t − 15) < 0
3 lip 19:26
Piotr: wyszło mi rownanie t3−4t−11t+30<0 , gdzie 5x=t i potem dalej robilem i zapisalem w postaci
iloczynowej wyszlo mi, ze (t−2)(t−5)(t+3)<0
3 lip 19:26
asdf: jeszcze jedno zalozenie o czym przypomniał ZKS, ale nie bede psuc zabawy

3 lip 19:26
Piotr: Tak samo mi asdf wyszlo

3 lip 19:26
Piotr: tylko zalozenia nie dalem : (
3 lip 19:27
asdf: w sumie nie trzeba dawać tego ostatniego założenia − można wywnioskować później

3 lip 19:27
ZKS:
Ale
Saizou ładnie rozwiązał nawet nie potrzebował wprowadzać nową zmienną
t.

Tylko na samym końcu się pomylił.
3 lip 19:28
ZKS:
Dobra ja już się nie udzielam bo to post
ICSP.

3 lip 19:30
Piotr: t∊(−∞,−3) U (2,5)
5x=t
t<−3
5x<−3
Brak rozwiazania
2<t<5 i 5x<5
5x>2 x<1
brak rozwiazania
3 lip 19:30
asdf: @Piotr
łatwiej:
5x = t
x = log5t
3 lip 19:32
Piotr: Tylko, ze ja jeszcze nie mialem logarytmów. Zaczelismy ledwo pod koniec czerwca. Wiem o co Ci
chodzi. Ale tym moim sposobem, to jak dalej to skonczyć?

3 lip 19:34
Saizou : 5x+3=0
5x=−3 sprzeczność
.....
x∊(log52:1)
3 lip 19:35
ZKS:
Saizou jest git.

3 lip 19:38
asdf: @Piotr
Jak nikt nie udzieli Ci wskazowki do godz. 22 to pomoge jak wroce.
3 lip 19:41
Piotr: Ok, dzięki

3 lip 19:41
ZKS:
Piotr skoro robisz te podstawienie to jakie jest t.
3 lip 19:45
Piotr: t >0 ?
3 lip 19:48
ZKS:
Dobrze więc teraz powinieneś sobie poradzić. Jak będą jakieś wątpliwości to pisz.
3 lip 19:54
Piotr: Ja musze iść, bede pózniej o 22.. Jezeli x=log5t to zgodnie z definicja logarytmu t > 0 ale
nie wiem czy to tak ma byc
3 lip 19:55
Piotr: Czyli to bedzie odpowiedz taka, ze x∊(0,1) ?
3 lip 19:56
Piotr: Sorry, to tak nie bedzie cofam wypowiedz ostatnia
3 lip 19:57
Piotr: Pomysle pozniej lub jutro bo juz nie mysle po prostu..

3 lip 20:00
ZKS:
Skoro rozwiązałeś nierówność tak to do tego należy dodać jeszcze jeden warunek
(t < −3 ∨ 2 < t < 5) ∧ t > 0
bierzemy część wspólną przedziałów i dostajemy
2 < t < 5.
Teraz wystarczy wrócić z podstawieniem i dokończyć rozwiązywanie tej nierówności.
3 lip 20:04
Piotr: Aha juz rozumiem.
2<5x<5
x>log52 i x<1
Robilem tak od samego poczatku tylko ''wywalielm to 2<5x bo w funckji wykladniczej sie tak
robilo. Mam pytanie odnosnie tego zalozenia, np na lekcji gdy wprowadzalismy zmienna
pomocnicza ''t'' i t=2x to nie pisalismy, ze t>0 . Nie wiem juz sam czy na lekcji zle
robilismy czy cos zle mysle
3 lip 20:42
Piotr: I wlasnie od samego poczatku mi wychodzilo, że x<1 bo nie uwzglednilem tej jednej rzeczy
3 lip 20:42
ZKS:
Kiedy w funkcji wykładniczej tak się robi że wyrzuca się nierówność 5x > 2?
3 lip 20:43
3 lip 20:45
ZKS:
Gdzie masz brak rozwiązań? Przecież dla x = 1 widać od razu że 5x > 2 jest spełnione więc jak
może być brak rozwiązań?
3 lip 20:47
Piotr: Faktycznie, ale i tak mi wszystko sie pomieszalo jakos teraz

3 lip 20:50
Piotr: Pewnie chcialem sprowadzić do jednakowych podstaw a liczby 5 nie da sie podnieść do
jakiejkolwiek potegi zeby dala 2 i dlatego tak myslalem
3 lip 20:54
ZKS:
| | 2 | |
Tam masz że 3x < − |
| a przecież wiesz że zbiór wartości funkcji y = 3x gdzie jest |
| | 3 | |
ZW = (0 ;
∞) czyli 3
x nigdy nie osiągnie wartości mniejszej lub równej zero zatem
| | 2 | |
3x nigdy nie będzie mniejsze od − |
| a co za tym idzie otrzymujemy brak rozwiązań. |
| | 3 | |
Rozumiesz?
3 lip 20:54
ZKS:
Jak to przecież 5log52 = 2.
3 lip 20:55
Piotr: Tak rozumiem juz. Jeszcze mam jedno pytanie odnosnie tego zalozenia zaraz Ci napisze przyklad z
lekcji

3 lip 20:55
ZKS:
Okej.

3 lip 20:56
Piotr: Tylko wiesz, ja mialem funkcje wykladnicza przed rozpoczeciem logarytmow(2 lekcje mialem
logarytmow) i dlatego tak myslalem ..

3 lip 20:56
Piotr: 4x−3*2x+2>0
(2x)2−3*22+2>0
t=2x
t2−3t+2>0
i ''t'' pozniej wyjdzie, ze t∊(−∞;1)U (2;∞)
t<1 v t>2
x<0 v x>1
I tutaj nie bylo zalozenia ze t>0 jest to przyklad z lekcji
3 lip 20:58
ZKS:
Chyba wszyscy tak mieli że funkcje wykładnicze były przed funkcjami logarytmicznymi.

3 lip 21:00
Piotr: Tak, i ja na poczatku myslalem inaczej ze nie da sie podnieść 5 do jakieś potęgi zeby otrzymac
2. Jakbys mogl to sprawdz ten przyklad

3 lip 21:01
ZKS:
Rozwiązanie końcowe jest poprawne ale niestety zapis nie. Zauważ że jeżeli
t < −2 to jest to sprzeczne.
t ∊ (−∞ ; 1) ∪ (2 ; ∞) ∧ t > 0 ⇒ t (0 ; 1) ∪ (2 ; ∞)
0 < 2x < 1 ∨ 2x > 2
2x > 0 ⇒ dla każdego x ∊ R
2x < 1 ⇒ x < 0
cześć wspólna x ∊ R ∧ x < 0 ⇒ x < 0
2x > 2 ⇒ x > 1
suma tych przedziałów to nasze rozwiązanie
x ∊ (−∞ ; 0) ∪ (1 ; ∞).
3 lip 21:06
ZKS:
No w sumie można tak zapisać jak na lekcji ale często właśnie później są jakieś błędy więc
lepiej od razu pisać założenia do tej zmiennej jaką wprowadzamy aby później nie dostać
jakieś głupoty.

3 lip 21:09
Piotr: No wlasnie przez to nie wprowadzilem tego zaloeznia cholernego... i tyle czasu nad tym
myslalem a wszystko dobrze bylo... Czyli bierzemy t>0 bo ZWf=(0,+∞), tak?
3 lip 21:13
3 lip 21:15
ZKS:
Przykładowo byś miał nierówność
4x + 3 * 2x + 2 > 0
2x = t (jeżeli nie damy że t > 0 to zobacz co można dostać jeżeli się zapomni o tym że t > 0)
t2 + 3t + 2 > 0
(t + 1)(t + 2) > 0
t ∊ (−∞ ; − 2) ∪ (−1 ; ∞)
t < −2 ∨ t > −1
2x < −2 ∨ 2x > −1
i teraz przeważnie dzieją się dziwne rzeczy ale jeżeli pamiętasz że 2x = t > 0
t ∊ (−∞ ; − 2) ∪ (−1 ; ∞) ∧ t > 0 ⇒ t > 0
2x > 0 ⇒ x ∊ R
albo
t ∊ (−∞ ; − 2) ∪ (−1 ; ∞)
t < −2 ⇒ 2x < −2 ⇒ brak rozwiązań ∨ t > −1 ⇒ 2x > −1 ⇒ x ∊ R
tutaj pamiętamy że 2x > 0 bez zapisywania tego 2x = t > 0.
Suma tych przedziałów to nasze rozwiązanie tak więc x ∊ R.
3 lip 21:17
ICSP: 4x + 3 * 2x + 2 > 2 > 0− zachodzi dla każdego x ∊ R
x ∊ R
po co Ci ta zmienna xD
3 lip 21:20
ZKS:
Nie musisz dawać tego założenia ale możesz o tym zapomnieć i dostać błędne rozwiązanie więc
błędem nie będzie jeżeli nie napiszesz tego założenia lub je napiszesz.
Mam nadzieję że teraz jest wszystko jasne.
3 lip 21:20
Piotr: ZKS mi tlumaczy jedna rzecz i dlatego taki przyklad dal

3 lip 21:21
ZKS:
Po to żeby wyjaśnić na prostym przykładzie.

3 lip 21:21
Piotr: Tak, dziękuję ZKS za poświęcony mi czas

3 lip 21:22
ZKS:
Na zdrowie.

Poproś
ICSP to Ci jeszcze da jakiś ciekawy przykład żebyś się nie nudził.

3 lip 21:24
3 lip 21:26
ICSP: | | (5x −5)(5x + 5) | |
5x + |
| > 0 |
| | 1 − 5x | |
i z równań :
8
2x+1 = 32 * 2
4x − 2
3 lip 21:27
Przyszły maturzysta:
26x * 8 = 8 * 24x
2x = t > 0
t6 − t4 = 0
t4(t − 1)(t + 1) = 0
t = 1 (reszta rozwiązań odpada) ⇒ x = 0
Dobrze ?
3 lip 22:29
ICSP: 
3 lip 22:30
Godzio:
ICSP przygotowywacz maturalny

3 lip 22:31
ICSP: Witaj
Godzio 
Dawno nie gadaliśmy. CO tam u Ciebie ? Jak sesja ?
3 lip 22:32
Piotr: ICSP zaraz wstawie rozwiazanie nierownosci wykladniczej

3 lip 22:44
asdf: @Piotr
nie chce mi sie czytac tego wszystkiego, poradziles sobie z tamtym?
3 lip 22:49
Piotr: Założenie:
1−5
x≠0
1≠5
x
x≠0 D∊R−∫0∫
| 5x(1−5x)+(5x−5)(5x+5) | |
| >0 |
| 1−5x | |
(5
x−25)(1−5
x)>0
5
x−25=0 1−5
x=0
x=2∊ do załozenia; x=0 < nie nalezy do zalozenia a więc:
(nie mialem jeszcze do konca logarytmow wiec nie wiem czy dobrze odczytam zbiori narysuje
wykres)
Odp: x∊(−
∞;2) hmm? czy na odwrot?
3 lip 22:53
Piotr: Tak poradzilem sobie juz z tamtym zadaniem. Po prostu myslalem ze 5
x>2 to bedzie brak
rozwiazan i w tym tkwil moj problem caly i dlatego sie nie zgadzalo z odpowiedzia

3 lip 22:53
ICSP: no to musisz sobie jeszcze z tym poradzić

3 lip 22:56
Piotr: Czyli mam dobrze wszystko oprocz odczytania zbioru rowiazan?
3 lip 22:57
ICSP: do momentu : (1 − 5x)(5x − 25) > 0 masz dobrze.
3 lip 22:58
Piotr: I teraz co powinienemn zrobic? Okreslic miejsca zerowe? Takiego czegos to nie mialem w szkole
chyba jeszcze
3 lip 22:59
ICSP: Nie miałeś jeszcze funkcji kwadratowej w szkole ?
3 lip 23:00
ICSP: no ale. Można robić powolutki i na logikę :
a*b > 0 ⇒ (a > 0 ∧ b > 0 ) v (a < 0 ∧ b < 0 )
3 lip 23:01
Piotr: Mialem funkcje kwadratowa

.Tylko, ze pierwszy raz spotykam się ze 'x' jest w wykladniku i ze
mam z tego podać zbior rozwiazan
3 lip 23:02
Piotr: Bo wczesniej to bylo , np x+4x−16 i takie tam a nie ze 'x' w wykladniku . Mialem funckje
wykladnicza ale nie okreslalem rozwiazan w nierownosci powyzszej
3 lip 23:06
ICSP: ale przecież jest taki sam przypadek. W danym miejscu funkcja przechodzi przez oś Ox i zmienia
znak. Tak samo jak w przypadku funkcji kwadratowej. Musisz wiedzieć tlyko jakie znaki są po
której stronie i możesz podać odpowiedź

3 lip 23:07
Piotr: Na logike latwiejszy dla mnie

a=5
x−25 i b=1−5
x
5
x>5
2 1>5
x
x>2 x>0
(gdyz to funcka rosnaca)
lub
5
x−25<0 i 1−5
x<0
x<2 i x<0
Po dokonaniu czesci wspolnej i sumy zbiorow odp to x∊R−∫2∫
3 lip 23:14
Piotr: Do poprawy znowu....no nie
3 lip 23:16
ICSP: 1 > 5
x ⇒ x > 0

Jesteś pewny ?
3 lip 23:23
Piotr: Juz wiem gdzie blad

x<0
Zaraz poprawie, tylko pewne papiery wypelnie wpierw
3 lip 23:28
Piotr: I przypadek:
x>2 i x<0
x∊ do zbioru pustego
II przypadek:
x<2 i x>0
x∊(0;2)
Odp:x∊(0;2), tak?
3 lip 23:31
ICSP: tak
3 lip 23:35
Piotr: Ok, dzięki za pomoc

3 lip 23:35
 1. Znajdź takie m aby nierówność była spełniona dla każdego x ∊ R :
1. Znajdź takie m aby nierówność była spełniona dla każdego x ∊ R :



 ?. Ja to
pomnozylem przez kwadrat mianownika, potem wprowdzilem za 5x=t ale i tak lipa ; /. Sprobuje
pozniej
?. Ja to
pomnozylem przez kwadrat mianownika, potem wprowdzilem za 5x=t ale i tak lipa ; /. Sprobuje
pozniej 



 Tylko na samym końcu się pomylił.
Tylko na samym końcu się pomylił.















 Poproś ICSP to Ci jeszcze da jakiś ciekawy przykład żebyś się nie nudził.
Poproś ICSP to Ci jeszcze da jakiś ciekawy przykład żebyś się nie nudził. 

 ICSP możesz dać jeszcze jakis przyklad
ICSP możesz dać jeszcze jakis przyklad  najwyzej go jutro rozwiaze ( poziom 1 i 2 klasa
liceum)
najwyzej go jutro rozwiaze ( poziom 1 i 2 klasa
liceum) 


 Dawno nie gadaliśmy. CO tam u Ciebie ? Jak sesja ?
Dawno nie gadaliśmy. CO tam u Ciebie ? Jak sesja ?



 .Tylko, ze pierwszy raz spotykam się ze 'x' jest w wykladniku i ze
mam z tego podać zbior rozwiazan
.Tylko, ze pierwszy raz spotykam się ze 'x' jest w wykladniku i ze
mam z tego podać zbior rozwiazan

 a=5x−25 i b=1−5x
5x>52 1>5x
x>2 x>0
(gdyz to funcka rosnaca)
lub
5x−25<0 i 1−5x<0
x<2 i x<0
Po dokonaniu czesci wspolnej i sumy zbiorow odp to x∊R−∫2∫
a=5x−25 i b=1−5x
5x>52 1>5x
x>2 x>0
(gdyz to funcka rosnaca)
lub
5x−25<0 i 1−5x<0
x<2 i x<0
Po dokonaniu czesci wspolnej i sumy zbiorow odp to x∊R−∫2∫
 Jesteś pewny ?
Jesteś pewny ?
 x<0
Zaraz poprawie, tylko pewne papiery wypelnie wpierw
x<0
Zaraz poprawie, tylko pewne papiery wypelnie wpierw
