am sds: Rysowanie wykresow funkcji http://i44.tinypic.com/xerbr4.jpg Nie wiem jak to narysowac, wydaje mi sie tylko ze nie ma punktu przegiecia bo f''(x)=/=0 w tym punkcie, moglby mi to ktos objasnic? szczegolnie kiedy funkcja jest maleja/rosnaca w zaleznosci od pochodnych

wredulus_pospolitus: f'(2) = 0 i wiesz że na lewo od x=2 pochodna ujemna ... a na prawo dodatnia w takim razie w x=2 co mamy

wredulus_pospolitus: a bywałeś/aś na cwiczeniach

sds: nie wiem, nie mialem cwiczen zadnych

wredulus_pospolitus: student

sds: aha, minimum lokalne?

sds: moglby mi to ktos naszkicowac?

Janek191: f : R → R f' ( x ) < 0 dla x > 2 f''(x) < 0 dla x ∊ R 1) f '(2) = 0 ∧ f''( 2) < 0 więc funkcja f posiada w x₀ = 2 maksimum lokalne 2) Funkcja f nie ma punktu przegięcia w x₀ = 2, bo f'' (2) < 0 czyli f'' (2) ≠ 0

sds: a jak ten wykres bedzie wygladal? bo mi wyszla ze to bedzie taka parabolka o a<0 i wierzcholku w punkcie x=2

Janek191: Dla x < 1 wykresem jest cżęść paraboli W = ( 1; 0)

	1
Dla x > 1 wykresem jest część hiperboli y =
	x − 1

Janek191: Pomyłka − to jest do innego zadania.

Janek191: Do zadania z 16.47

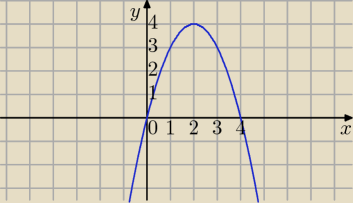
Mila: wykres 15:01 np. f(x)=−x²+4x f'(x)=−2x+4 −2x+4=0⇔x=2 −2x+4<0 −2x<−4 x>2 f''(x)=−2<0 dla x∊R

sds: Mila czyli obojetnie gdzie wierzcholek, chodzi tylko o taka parabolke tak?

sds: tzn obojetny y wierzcholka

Mila: Zgadza się.

sds: Dzięki, a jeżeli chodzi o to: http://tinypic.com/view.php?pic=xd5yyx&s=5 to jak mam rozumieć ten zapis lim(f(x) − x)= ∞. Jak do wykresu ma sie ta zaleznosc?

Mila: 1) f(x) ma prawostronną asymptotę w 1 2)lim{x→∞}f(x)=0 oznacza asymptotę poziomą y=0 3)lim{x→−∞}(f(x)+x)=∞ tu badana jest asymptota ukośna: y=ax+b

	f(x)
a=lim{x→−∞}		=−1
	x

b=lim{x→−∞}(f(x)−ax)=lim{x→−∞}(f(x)+x)=∞ zatem nie ma asymptoty ukośnej ( powinna wyjść stała)