Iwan: i też mam to samo pytanie co do tego zadania mam tu trochę kłopotów:
no i wychodzi mi tu że
i co dalej bo mam kłopoty z ogarnięciem tego
proszę o pomoc
Mila:
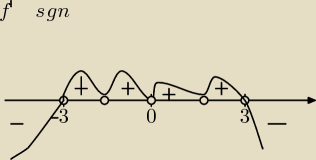
1)
D:
x≠
√3 i x≠−
√3
| | 3x2*(3−x2)−x3*(−2x) | |
f'(x)= |
| = |
| | (3−x2)2 | |
Ekstrema:
9x
2−x
4=0⇔
x
2*(9−x
2)=0
x=0 lub x=3 lub x=−3
f'(x)>0 ⇔funkcja jest rosnąca
f'(x)<0⇔funkcja jest malejąca
9x
2−x
4>0
x
2*(3−x)*(3+x)>0
miejsca zerowe:
x=0 podwójny, x=3, x=−3 dla x=
√3 i x=−
√3 pochodna nieokreślona
funkcja malejąca w przedziałach: (−
∞,−3)∪(3,
∞)
dla x∊(−3,−
√3)∪(−
√3,0)∪(0,
√3)∪ (
√3,3)funkcja rosnąca
w x=−3 funkcja ma minimum lokalne,y
min=4,5 pochodna zmienia znak przy przejściu przez x=−3
w x=3 funkcja ma maksimum lokalne y
max=−4,5
Narysuję wykres f(x) w następnym wpisie.


 wyliczona
za coś takiego powinni ze studiów wywalać
wyliczona
za coś takiego powinni ze studiów wywalać
 1)
1)
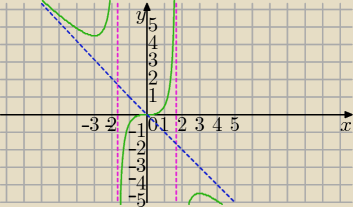 1)
1)