nieskończoność obi2exe: Nieskończoność to dla absolwenta szkoły średniej temat dziura. Zagadnienie przewróconej ósemki jest przez nauczycieli pomijane i najczęściej jego wyjaśnienie sprowadza się do kilku niewyczerpujących słów. Tak czy inaczej w ostatnim czasie interesuję mnie granica ciągu. W prawdzie prawie mam to już "jaskrawe", ale pozostała sprawa związana z rachunkami, w których występuje nieskończoność. Czy mógłby ktoś pokazać jak mnożyć nieskończoność dla przykładu z zerem, liczbą ujemną, pierwiastkiem itd... Co z odejmowaniem i dodawaniem i jak ma się do tego przewrócona ósemka.

use: otóż w granicach mozesz wyjsc na cos co sie nazywa SYMBOLEM NIEOZNACZONYM przykładowo jak otrzymasz [∞*0] to jest to symbol nieoznaczony i nie wiemy do czego to zmierza wiec trzeba cos z tym

	0		∞
zrobic najlepiej doprawadzic do sytuacji [		] albo [		] i liczyc granice Hospitalem
	0		∞

, jednak to wymaga znajomosci pochodnych Wsumie to dziwne pytanie zadales bo jezeli chodzi o odejmowanie czy dodawanie to cokolwiek odejmiesz od ∞ ( prucz oczywiscie ∞) to to nadal bedzie ∞ , podobnie z dodawaniem

PW: "Nieskończoność" nie jest liczbą, nie są określone dla tego pojęcia żadne działania. Wszelkie napisy typu "∞+∞" czy "∞•0" są umownym zapisem − skrótem myślowym, nie oznaczają działania arytmetycznego..

use: dokładnie tak jak powiedział PW są to TYLKO SYMBOLE ktorych sie uzywa dla ulatwienia po prostu

obi2exe: Ok. Jednak na tej stronie spotkałem się z zapisem ∞ razy (−3) == −∞ dlaczego

asdf:

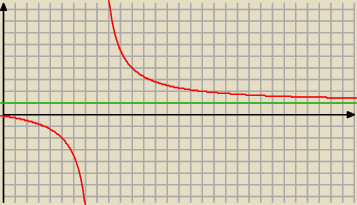
	1		1
w granicach ciągu wyniki takie jak		,		,....,log2, e423 itd itd..określają
	2		234234

wartość funkcji do jakiej się zbliża przy nieskończonych argumentach n. dla prostego rachunku, policz sobie granicę:

	n+1
limn→∞		= 1 (graficznie udowodnione nawet)
	n−8

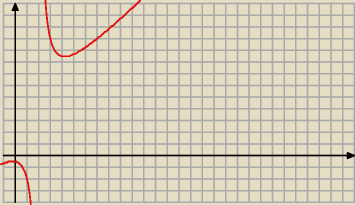
asdf: symbol ∞ określa wartości osiągane przy argumentach n dążących ∞, np funkcja:

	n2+1
limn→∞		, początkowo osiąga ona wartości ujemne...natomiast to co istotne do
	n−2

badania ciągu jest fakt granicy w nieskończoności. Na rysunku tego nie widac, ale tak jest − funkcja dalej nigdy się, ani nie przegnie, ani nie zmieni monotoniczności. po prostu dla każdego kolejnego argumentu n funkcja osiągać będzie większe wartości.

Trivial: asdf, ja na tym wykresie nie widzę czemu ten iloraz ma być niby 1

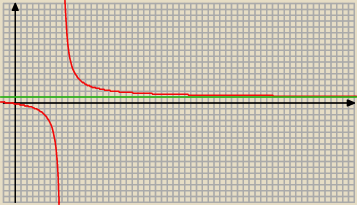
asdf: ja też nie to ma dążyć do 1

Trivial: wow. dziś nie myślę.

obi2exe: Ok. Jednak na tej stronie spotkałem się z zapisem ∞ razy (−3) == −∞ dlaczego Nie zobaczyłem analogii.

asdf: jak tam po sesji? Postawiłem sobie za cel, ze nie bede nic robic przez najblizsze 2 tygodnie, chyba nie podołam

Trivial: zapis ∞*(−3) = −∞ to nie jest formalny zapis. to tylko intuicja. Bierzemy bardzo dużą liczbę dodatnią, mnożymy przez −3 i otrzymujemy bardzo dużą (na moduł) liczbę ujemną.

asdf: @obi2exe wartość danego wyrażenia jest ujemna, gdy ilość występujących przy liczbach minusów jest nieparzysta, np. −1 * 3 = −3 −1 * (−31230123012) = 31230123012 −1 * (−31230123012) * (−1) = −31230123012 nie da się prościej

asdf: może nie ilość występujących minusów, a wartości, bo np.

	1
log4(		) * ∞ = −∞
	2

ale chyba nie musze tego wyjasniac − wiesz o co chodzi..

obi2exe: "zapis ∞*(−3) = −∞ to nie jest formalny zapis. to tylko intuicja. Bierzemy bardzo dużą liczbę dodatnią, mnożymy przez −3 i otrzymujemy bardzo dużą (na moduł) liczbę ujemną." − tak rozumiem, dzięki. @asdf − nie wiem co chcesz tym wytłumaczyć? Chodzi Ci o to, że dwa minusy to plus? Tak?

asdf: tak − dwa minusy to plus, chociaż w ostatnim przykładzie Ci udowodniłem, że tak nie jest, np.

	1
log4(		) * √e jest mniejsze od zera...chodzi bardziej o wartości przy każdym wyrażeniu.
	2

obi2exe: Aha, takie przykłady są chyba oczywiste, z tą nieskończonością też tak myślałem, ale lepiej się upewnić zanim coś wejdzie w krew. Dzięki.