Zaznacz na płaszczyźnie współrzędnych zbiory punktów.
wajdzik: Zaznacz na płaszczyźnie współrzędnych zbiory punktów, których współrzędne spełniają poniższe
nierówności:
(x+|x|)
2+(y+|y|)
2≤16
Rozpiszę tą nierówność na 4 przypadki:
I przypadek
x≥0 y≥0
(2x)
2+(2y)
2≤16
4x
2+4y
2≤16
x
2+y
2≤4 /
2
x+y≤2
y≤2−x
II przypadek
x≥0 y<0
(2x)
2≤16
4x
2≤16
x
2≤4
x≤2
III przypadek
x≤0 y≥0
y≤2
IV przypadek
x<0 y<0
0≤16
Sprzeczność.
Czy to jest dobrze rozwiązane? Mogę przejść do narysowania rysunku?

2 lip 17:33
ZKS:
Multum błędów.
2 lip 17:40
Aga1.: Źle, np
x2+y2≤4 −jest to koło ośrodku (0,0) i promieniu 2
x2≤4
IxI≤2
−2≤x≤2
2 lip 17:40
ZKS:
Od kiedy √x2 + y2 = x + y?
2 lip 17:40
ZKS:
Żaden przypadek niestety nie zrobiłeś poprawnie.
2 lip 17:42
wajdzik: Ok, od początku.
2 lip 17:43
wajdzik: I przypadek:
x≥0 i y≥0
(2x)2+(2y)2≤16
4x2+4y2≤16
x2+y2≤4
Otrzymujemy koło o środku (0,0) i promieniu r=2
Jak już napisała Aga.
2 lip 17:45
wajdzik: II przypadek:
x≥0 y<0
4x2≤16
x2≤4
|x|≤2 ⇔ −2≤x≤2
2 lip 17:47
wajdzik: III przypadek:
−2≤y≤2
2 lip 17:48
ZKS:
Jeszcze dokończ ten II przypadek masz warunek że x ≥ 0 oraz y < 0 uwzględnij to.
2 lip 17:49
ZKS:
III przypadek identycznie.
2 lip 17:49
wajdzik: IV przypadek:
0+0≤16
0≤16 −> zgadza się, 0 jest mniejsze od 16.

Mam nadzieję, że teraz wszystko jest ok. Biorę się za rysowanie
2 lip 17:50
wajdzik: Ok, już dokończę.
2 lip 17:50
Aga1.:
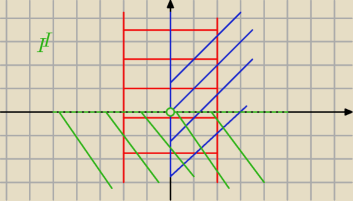
2 lip 17:52
wajdzik:
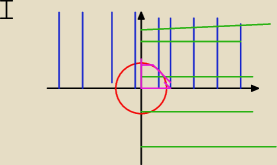
Część wspólna oznaczona na różowo.
Widzę Ago, że we mnie nie wierzysz, spokojnie, poradzę sobie.

2 lip 17:59
wajdzik: Ago, zrobiłaś III przypadek bo tam miałem x<0, II już robię.
2 lip 18:00
Aga1.: Jestem pewna, że opanujesz ten temat.
Trochę z nudów , narysowałam drugi przypadek, a nie trzeci.
2 lip 18:06
wajdzik:
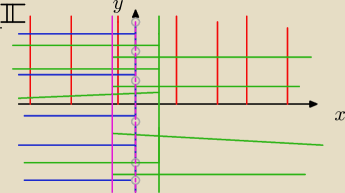
Różowy kolor to część wspólna.
2 lip 18:07
wajdzik: ja cały czas pracuję(bo wakacje teraz), w wolnej chwili jak tylko taką znajdę to robię
2 lip 18:09
wajdzik:
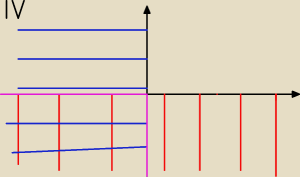
Częścią wspólną jest III ćwiartka.
2 lip 18:12
wajdzik: Odpowiedź: Rozwiązaniem jest suma rozwiązań.
Dzięki za pomoc.
2 lip 18:13
Aga1.:
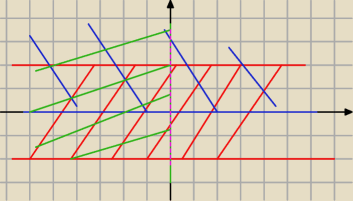
Trzeci przypadek wygląda tak
x<0
y≥0
−2≤y≤2
Pierwszy i czwarty zgadza się.
2 lip 21:50

 Mam nadzieję, że teraz wszystko jest ok. Biorę się za rysowanie
Mam nadzieję, że teraz wszystko jest ok. Biorę się za rysowanie

 Część wspólna oznaczona na różowo.
Widzę Ago, że we mnie nie wierzysz, spokojnie, poradzę sobie.
Część wspólna oznaczona na różowo.
Widzę Ago, że we mnie nie wierzysz, spokojnie, poradzę sobie. 
 Różowy kolor to część wspólna.
Różowy kolor to część wspólna.
 Częścią wspólną jest III ćwiartka.
Częścią wspólną jest III ćwiartka.
 Trzeci przypadek wygląda tak
x<0
y≥0
−2≤y≤2
Pierwszy i czwarty zgadza się.
Trzeci przypadek wygląda tak
x<0
y≥0
−2≤y≤2
Pierwszy i czwarty zgadza się.