całki Angela: Jak wyznaczyć granice całkowania obszaru ograniczonego takimi liniami: y=e^x x=1 y=(x−1)²

Angela: oraz granice takiego obszaru y²=2x+1 x−y−1=0

Janek191: y = e^x y = ( x − 1)² x = 1 e^x = ( x − 1)² ⇒ x = 0 czyli P = ∫₀¹ [ e^x − ( x − 1)²] dx =

Angela: a jak liczysz, że wychodzi Tobie tego równania x = 0

AS: Jedyny sposób jaki dostrzegam,to rozwiązać graficznie. Sporządzić wykres funkcji f(x) = e^x i f(x) = (x − 1)² w jednym układzie współrzędnych i znaleźć punkt wspólny. Jest nim (0,1)

Angela: dobra już wiem, pomyliłam się przy rysowaniu i dlatego nic mi nie wychodziło

Angela: a jeżeli chodzi o taki obszar y²=2x+1 x−y−1=0 jakie będą jego granice?

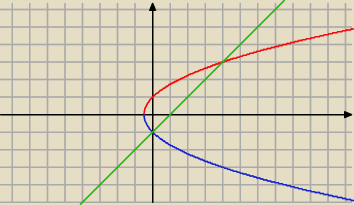
asdf: y = √2x+1 lub y = − √2x+1 x−y−1 = 0 ⇒ y = x−1

asdf: na wykresie widac, ze istotna jest jedynie krzywa czerwona i zielona, czyli: x−1 = √2x+1 //² (x−1)² = 2x+1 x²−2x+1 = 2x + 1 x²−4x=0 x(x−4)=0 x=0, x= 4 granice całkowania: dolna: x = 0, gorna: x=4 z gory ograniczone przez funkcję y = √2x+1 z dolu ograniczone przez funkcję: y = x−1 reszte samemu

asdf: tylko jeszcze musisz rozpatrzeć (dodać) ten malutki kawałek co jest pod OX na szczęscie

	1
widać, że jest to trójkąt, więc +		będzie ok, jak napiszesz stosowny komentarz
	2

Angela: to jak będzie wyglądała całka do rozwiązania tego?

Angela: ok rozumiem

Angela:

	1
wynik to powinno być 5		a mi wychodzi zupełnie co innego
	3

asdf: to moze obliczenia? Gotowca nie dostaniesz..

Angela: ∫₀⁴ √2x+1 − (x−1) dx = ∫₀⁴ √2x+1 − x + 1 dx

	1		1
∫√2x+1= t=2x+1 =		∫t12 dt =		(2x+1)32
	2		3

	dt
dx=
	2

1		1		1
	(2x+1)32 − ∫xdx + ∫dx =		(2x+1)32 −		x2 + x
3		3		2

	1		1		1		2
[		(2x+1)32 −		x2 + x ]04 = [9−8+4]−		= 4
	3		2		3		3

	1
I teraz do wyniku dodaje		czy gdzieś wcześniej..?
	2

Angela:

asdf: tak, do tego wyniku dodajesz 1/2

asdf:

	2		1		2		1		4		3		7		1
4		+		= 4 +		+		= 4 +		+		= 4 +		= 5
	3		2		3		2		6		6		6		6

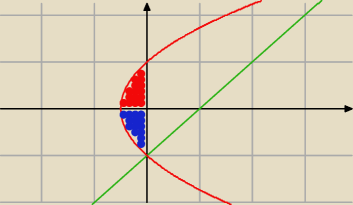
asdf: dodatkowo jeszcze musisz wziąć pod uwagę ten kawałek: √2x+1 = 0 2x+1 = 0 2x=−1

	1
x= −
	2

	1
z dolu przez −		, z gory przez 0 i teraz policz całkę (czerwony obszar):
	2

∫_−1/2|⁰ √2x+1dx = ... pomnozyc * 2 (bo niebieski tez trzeba uwzglednic − a jest taki sam) = wynik, i ten wynik dodać jeszcze do tej całki

asdf:

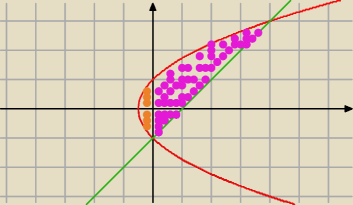
	1
sorry..wprowadziłem Ciebie w błąd nie trzeba dodawać		− bo to juz jest w całce:
	2

∫√2x+1 − (x−1) dx jak na razie masz policzone:

	2
różowy obszar = 4
	3

potrzebujesz pomarańczowy obszar (jak go obliczyc? − post wyzej)

	2		2
czyli na razie masz 4		, jak teraz wyjdzie te pomaranczowe pole powinno wyjść		,
	3		3

	1
czyli dwie połówki po
	3

Angela: super, nie dość że rozumiem to jeszcze idealnie wyszło dzięki!