calki - pole obszaru agata: Oblicz pole obszaru ograniczonego krzywymi: y²=x oraz y=x−2 Bardzo proszę o pomoc i krotkie wyjasnienie.

agata: czy moglby mi ktos pomoc...

AS: Punkt 1 Wyznacz punkty wspólne krzywej i prostej (x− 2)² = x ⇒ x1 = 1 , x2 = 4 Punkt 2 Oblicz pole pod krzywą w przedziale <0,4> (= P1) Punkt 3 Oblicz pole pod prostą w przedziale <1,4> (= P2) Punkt 4 Szukane pole P = P1 − P2 (= 55/3)

AS: Poprawka: P = 7/3

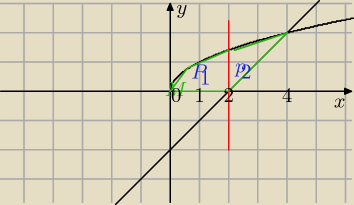
agata: musze obliczyc pole narysowane na zielono, tak? czy moge podzielić je na dwa (takie odzielone czerwona linia)? i obliczyc calke dla p1 ograniczona od 0 do 2 z √x − (y=0) oraz pole p2 czyli calke ograniczoną od 2 do 4 z √x − (x−2) a na koncu zsumować oba pola?

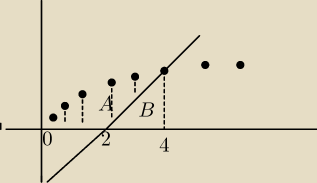
AS: Nie Obszar A pod krzywą w przedziale 0 − 4 Obszar B pod prostą w przedziale 2 − 4 Szukane pole P − A I jeszcze jedna poprawka − ostateczne pole P = 10/3 (co nagle to po diable)

AS: Szukane pole P = B − A

agata: dziekuje

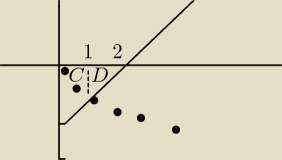
AS: Rozwiązanie moje nie jest pełne − nie uwzględniłem obszaru pod osią Ox Obliczam pole obszaru C

	−2		2
P3 = |∫01(−√x)| = |		*x*√x|01 =
	3		3

Pole obszaru D

	1		1
P4 = |		*1*(−1)| =
	2		2

Pole C + D

	1		7
P5 = U{2}{3| +		=
	2		6

Ostatecznie całe szukane pole

	7		27
Pc = U{10}{3) +		=
	6		6

Przepraszam za chaos w rozwiązywaniu − winien pośpiech.

pigor: ..., lub np. tak y²=x i y=x−2 ⇔ y²= y+2 /*4 i x= y+2 ⇒ 4y²−4y−8= 0 ⇔ (2y−1)²=9 ⇔ ⇔ |2y−1|=3 ⇔ 2y−1=−3 lub 2y−1=3 ⇔ 2y= −2 lub 2y= 4 ⇔ y= −1 lub y= 2 ⇒ ⇒ (x,y)= (1,−1) lub (x,y)= (4,2) − punkty przecięcia się wykresów x=y² i x=y+2, a pole między nimi względem osi OY wyrazić mogę wzorem : P= ∫ ²₋₁ (y+2−y²)dy= (¹₂y²+2y−¹₃y³) | ²₋₁= = 2+4−⁸₃− (¹₂−2+¹₃)= 6−⁸₃−¹₃+1,5= 6−3+1,5= 4,5 − szukane pole.

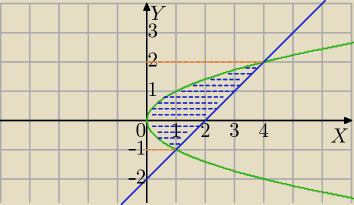
Mila: y²=x y=x−2 Wygodniej całkować po zmiennej y ( patrz wpis Pigora) Granice całkownia: y=y²−2⇔ y²−y−2=0 y₁=−1 lub y₂=2 y=x−2 i y²=x⇔ x=y+2 i x=y² P=₋₁∫²(y+2−y²)dy wynik u Pigora)

agata: aha, dzieki, ja myslalam ze funkcje y²=x czyli y=√x należy rysować tylko nad osia x − czyli tylko jedno (dodatnie) ramie paraboli. dlatego, pole obszaru chcialam liczyc tylko do tej osi

Mila:

Mila: y²=x to wzór opisujący krzywą (parabola)