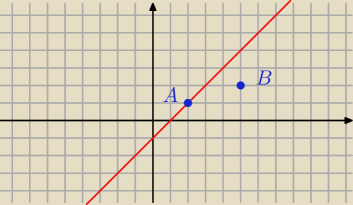
Aksjomat bezendu: Dane są punkty A=(2,1) i B=(5,2) Na prostej o równaniu x−y+1=0 wyznacz punkt M aby pole trójkąta MAB było równe 5 x−y−1=0 −y=−x+1 y=x−1 |AB|=√(5−2)²+(2−1)²=√3²+1=√10 a=√10

	1
P=		*√10h=5
	2

√10
	h=5
2

h=√10 i jak dalej ruszyć to zadanie ?

Dominik: przydatny moze byc wzor na pole trojkata z uzyciem wektorow. poszukaj, jest w tablicach maturalnych.

bezendu: właśnie tablice dzięki Dominik

bezendu:

	1
P=		|(xb−xa)(yc−ya)−(yb−ya)(xc−xa)|=5
	2

1
	|(5−2)(yc−1)−(2−1)(xc−1)|=5
2

1
	|3yc−3−(xc−1)|=5
2

1
	|3yc−3−xc+1|=5
2

1
	|3y−xc−2|=5
2

1
	|3(yc−1)−(xc−1)|=5
2

Mila: Może lepiej będzie, gdy obliczysz odległość punktu B od prostej, to będzie wysokość. obliczysz jaka długość AC i dalej okrąg........ Powinny byc dwa rozwiązania. A w ogóle, to jakie jest równanie prostej? Jeśli takie x−y+1=0, to A nie leży na tej prostej i zmienia się sytuacja.

bezendu: x−y−1=0

Mila: To zrób jak podpowiedziałam.

bezendu: ok

bezendu: odległość punktu B od prostej x−y−1=0

	5−2−1
h=		=√2
	√12+(−1)2

ale coś tu się nie zgadza skoro a=√10 h=√2 to pole jest=√5

Mila: A=(2,1) i B=(5,2), x−y−1=0

	|5−2−1|
h=
	√2

	2
h=		=√2
	√2

	1
PΔ=		*|AC|*√2
	2

1
	*|AC|*√2=5
2

√2*|AC|=10 /*2 2|AC|=10√2 |AC|=5√2 (x−2)²+(y−1)²=(5√2)² i y=x−1 M=(7,6) M₁=(−3,−4)

bezendu: Dziękuje bardzo

bezendu: Wykaż, że równanie nie ma rozwiązań w zbiorze liczb rzeczywistych:

	x
x2−x+1=
	x+1

D=R\{−1} (x²−x+1)(x+1)=x x³+x²−x²−x+x+1=x x³−x+1=0 pierwiastkiem tego wielomianu może być albo 1 albo −1 (−1∉D) w(1)=1³−1+1=1 czy to wystarczy ?

bezendu: Oblicz sumę wszystkich liczb naturalnych mniejszych od 10 000, które są podzielne przez 4 i których cyfrą jedności jest 6 a₁=16 a_n=9996 a₂=36 r=20 16+(n−1)*20=9996 16+20n−20=9996 20n=10000 n=500

	16+9996
S500=		*500=2503000
	2

Mila: x³−x+1=0 równanie ma jedno rozwiązanie rzeczywiste. Równanie nie ma rozwiązań wymiernych.

asdf: zeby wykazywac takie rzeczy jak "brak pierwiastkow, jedno rozwiazanie itd.." − bardzo przydatne są pochodne, warto jest się ich nauczyc − nie jest to nic trudnego, a znacznie przyspieszają rachunki.

Dominik: co do posta z 21:20 zauwaz, ze y_c = x_c + 1. jesli wszystkie przeksztalcenia wyzej byly prawidlowe to powinno pyknac.

bezendu: czyli równanie to nie ma też rozwiązań całkowitych?

Mila: C⊂W

bezendu: to chyba coś jest nie tak w tym zbiorze poszukam jutro tego zadania w starszym wydaniu. Dobranoc i dziękuję za pomoc

Mila: Może coś przekręciłeś w treści?

Saizou : bezendu to zadanie z zielonego Aksjomatu

ZKS: x₁ = 2 ; y₁ = 1 ; y₂ − y₃ = 2 − (x − 1) = 3 − x x₂ = 5 ; y₂ = 2 ; y₃ − y₁ = x − 1 − 1 = x − 2 x₃ = x ; y₃ = x − 1 ; y₁ − y₂ = 1 − 2 = −1 warunek ∑ y_{n + 1} − y_{n − 1} = 0 3 − x + x − 2 − 1 = 0 zatem ok liczymy pole ze wzoru |x_n(y_{n + 1} − y_{n − 1})| = 2P |2(3 − x) + 5(x − 2) + x * (−1)| = 2 * 5 |6 − 2x + 5x − 10 − x| = 10 |2x − 4| = 10 |x − 2| = 5 x − 2 = 5 ∨ x − 2 = −5 (x = 7 ∧ y = 6) ∨ (x = −3 ∧ y = −4) Ten wzór to nic innego jak ten z tablic tylko trochę przekształcony. Miałem go na geodezji więc go zapamiętałem bo mi się spodobał.

ZKS: Oczywiście zabrakło mi znaczka sigma przy wzorze do pola. | ∑ x_n(y_{n + 1} − y_{n − 1}) | = 2P

bezendu: Saizou czerwony aksjomat

Saizou : W(x)=x³−x+1=0 równanie 3 stopnia ma przynajmniej jeden pierwiastek rzeczywisty, jeśli nie jest nim rozwiązanie W(−1) to oznacza że W(x) ma przynajmniej jeden pierwiastek W(−1)=−1+1+1=1 zatem dowód jest fałszywy czy jakoś tak

bezendu: Mila znalazłem starsze wydanie w pdf tego aksjomatu i polecenie jest

	x
wykaż, że równanie x2−x+1=		nie ma rozwiązań w zbiorze liczb całkowitych
	x+1

Saizou : 22:04 o tej godzinie napisałeś że nie ma rozwiązanie w zbiorze liczb rzeczywistych więc wystarczy skorzystać z tw. o pierwiastkach całkowitych wielomianu o współczynnikach całkowitych i pokazać że takich pierwiastków nie ma

bezendu: a widziałeś post 22:45 w starszym zbiorze mam w zbiorze liczb całkowitych

Saizou : błąd w druku

bezendu: najwidoczniej ale w internecie również znalazłem wersje z liczbami rzeczywistymi ? czyli jak w zbiorze liczb całkowitych, to wtedy moje rozwiązanie 22:04 jest prawidłowe

bezendu: ?

Mila: Nie ma rozwiązań w zbiorze liczb całkowitych. Gdyby takie istniały, to mogłyby to być liczby ze zbioru {1,−1} a nie są.

bezendu: Czyli −1 odpada bo ∉D i sprawdzam tylko W(1)≠0 więc nie ma rozwiązań w zbiorze liczb całkowitych ?

Mila: Tak.

bezendu: Dziękuje, mam jeszcze jedno zadanie ? Miałabyś chwilę czasu teraz, albo wieczorem ?

Mila: Tak, nie przejmuj się, gdy nie odpowiem zaraz, bo odwołują mnie od komputera. Pisz.

bezendu:

	2
Dana jest funkcja		wykaż, że wykres tej funkcji jest symetryczny względem prostej
	x2−4x

x=2 x²−4x≠0 x(x−4)≠0 D=R\{0,4} Narysować ten wykres funkcji i prostą x=2 ? A może da się to zrobić bez rysowania ?

ZKS: Może przesunąć o 2 jednostki w lewo ten wykres wtedy osiami współrzędnych będzie y = 0 oraz x = 2 i wtedy pokazać parzystość tej funkcji?

	2
f(x) =
	x2 − 4x

	2
f(x) =
	x(x − 4)

	2
f(x + 2) =
	(x + 2)(x − 2)

Niech f(x + 2) = g(x) warunek parzystości funkcji g(x) = g(−x)

	2
g(−x) =
	(−x + 2)(−x − 2)

	2
g(−x) =
	−(x − 2) * −(x + 2)

	2
g(−x) =
	(x − 2)(x + 2)

g(x) = g(−x). Tylko co do tego sposobu nie mam pewności niech to ktoś zatwierdzi lepiej.

ZKS: Trochę namieszałem jeżeli przesuniemy ten wykres o 2 jednostki w lewo to wtedy wykres ten będzie symetryczny względem osi OY i wtedy należy zbadać parzystość tej funkcji czy aby na pewno wykres ten jest symetryczny względem prostej x = 2.

Mila: 1) Wyprowadź wzór opisujący przekształcenie płaszczyzny przez symetrię osiową względem prostej : x=2

	2
2) Znajdź wzór funkcji g(x) po przekształceniu f(x)=		przez tę symetrię.
	x2−4x

Powinno wyjść: g(x)=f(x) Skąd masz to zadanie?

Mila: Teraz u mnie kolacja. Będę później.

bezendu: Zadanie które zamieszczam ostatnim czasem pochodzą z czerwonego aksjomatu

bezendu: Miałem symetrię względem osi OY,OY, względem punktu ale nie wiem jak względem prostej..

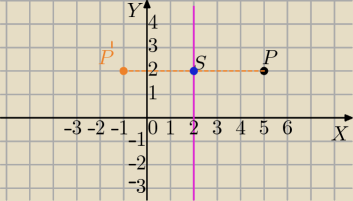
Mila: 1) symetria względem prostej x=2 x=2 oś symetrii P(x,y)− dany punkt P'(x',y')− punkt symetryczny do P(x,y) względem prostej x=2 y'=y S=(2,y) jest środkiem PP'

	x'+x
2=
	2

x'+x=4 x'=4−x Szukane przekształcenie: x'=4−x i y'=y

	2
2) przekształcenie funkcji: f(x)=y=
	x2−4x

	2
y'=
	(4−x')2−4(4−x')

dokończ i opuść znaczki '

Mila: Wyjaśnienie: Do wzoru funkcji f(x) podstawiamy y' za y, następnie wyznaczamy x: x'=4−x to x=4−x' Do wzoru funkcji podstawiamy 4−x' za x.

bezendu:

	2
y=
	16−8x+x2−16+4x

	2
y=
	x2−4x

Mila: Wniosek: wykres f(x) jest symetryczny względem prostej x=2.

bezendu:

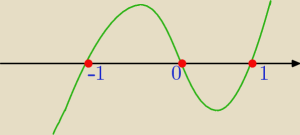
	x3
Dana jest funkcja f(x)=
	x2−1

a) wykaż, że wykres tej funkcji jest symetryczny względem początku układu współrzędnych b) wyznacz te wartości x dla których zachodzi nierówność f(x)≥0 a) −f(−x) ? wystarczy to zastosować ? b) D=R\{−1,1} x³(x²−1)≥0 x³(x−1)(x+1)≥0 x∊(−1,0>∪(1,∞)

Aga1.: a)Tak. Wykaż,że f(x)=−f(−x) b)ok.

bezendu:

	x3
f(x)=
	x2−1

	(−x)3		−x3		x3
−f(−x)=−(		)=−(		)=
	(−x)2−1		x2−1		−x2+1

−x3
x2−1

zgadza się ?

bezendu: poprawka

	(−x)3		−x3		x3
−f(−x)=−		=−		=
	(−x)2−1		x2−1		x2−1

czyli jak f(x)=−f(−x) to znaczy, że jest symetryczny względem początku układu współrzędnych ?

bezendu: Jeszcze pytanie: Jeśli mam zadanie typu: Wykaż, że wykres jest symetryczny względem.... to zawsze wykres dany w zadaniu musi się równań wykresowi funkcji po odpowiednim przekształceniu ?

Mila: Tak. Figury symetryczne są przystające.

bezendu: Dziękuję