dziękuję :): zlokalizuj liczbę zespoloną z=√3 − i na płaszczyżnie zespolonej.Przedstaw w postaci trygonometrycznej i oblicz z⁵

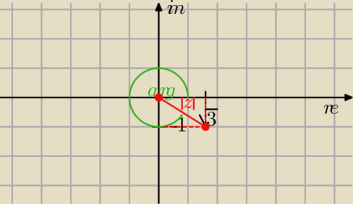
123: z⁵ = (√3 − i)⁵ Trzeba skorzystać ze wzory de Moivre'a. 1. Przekształcamy na postać trygonometryczną |z| = √√3² + (−1)² = √9 + 1 = √10

	√3		√30
cos φ =		=
	√10		10

	1		√3
sin φ = −		= −
	√3		3

	√3
IV ćwiartka i α0 = arcsin
	3

	√3
Zatem φ = 2π − arcsin
	3

	√3		√3
z = √10(cos(2π − arcsin		+ isin(2π − arcsin		)) − postać trygonometryczna
	3		3

z⁵ = |z|⁵(cos(nφ) + isin(nφ))

	√3		√3
(√3 − i)5 = (√10)5[cos(10π − 5arcsin		) + isin(10π − 5arcsin		)]
	3		3

123:

	1
Oj tam sinus φ = −
	√10

123: Ale reszta dla takiego czegoś jest ok

:): bardzo dziękuję

Janek191: z = √3 − i więc I z I = √ (√3)² + (−1)² = √3 + 1 = √4 = 2

	√3
cos φ =
	2

	−1
sin φ =
	2

więc

	π		11
φ = 2π −		=		π
	6		6