Zaznacz na płaszczyźnie współrzędnych zbiory punktów. wajdzik: Zaznacz na płaszczyźnie współrzędnych zbiory punktów, których współrzędne spełniają poniższe nierówności. y+|y|−x−|x|<0 y+y−2−x<0 ⋀ |y|−|x|≥0 ⋁ y−y−x+x<0 ⋀ |y|−|x|<0 ⇔ ⇔2y−2x<0 ⋀ |y|≥|x| ⋁ 0<0 ⋀ |y|<|x| ⇔ ⇔ y<x ⋀ |y|≥|x| ⋁ x∊∅ robiłem też innym sposobem(swoim) gdzie wyszło mi, że: x>0 y<0 x<y x∊∅ i suma mi wyszła taka: I ćwiartka w układzie współrzędnych. Skorzystałem również z Wolfram|Alpha: http://www.wolframalpha.com/input/?i=y%2B%7Cy%7C-x-%7Cx%7C%3C0 Czekam na odpowiedź.

wredulus_pospolitus: y+|y| < x+|x| dla y>0 masz:

	x+|x|
2y < x+|x| −> y <
	2

czyli dla y>0 i x>0 −>>> y<x (czyli obszar w I ćwiartce 'pod' wykresem y=x) czyli dla y<0 i x<0 −>>> y<0 <−−−brak rozwiązań dla y<0 0 < x+|x| czyli dla y<0 −−−> x>0 (cała ćwiartka IV)

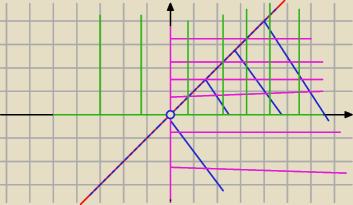
Aga1.: Rozpisałabym na 4 przypadki I . y≥0 x≥0 y<x rozwiązanie tam ,gdzie pokrywają się trzy kolory.

Aga1.: II. y≥0 x<0 y<0 sprzeczność III. y<0 x≥o x>0 Rozwiązaniem 4 ćwiartka. IV. y<0 x<0 0>0 sprzeczność ostatecznie Końcowym rozwiązaniem jest suma rozwiązań.

wajdzik: Dzięki za pomoc