zastosowanie calek artur: oblicz objętość bryły która powstaje przez obrót dookoła osi OX figury ograniczonej krzywymi o równaniach y=x² i x=y².

AS: Szukam punktu wspólnego dla obu krzywych x² = x⁴ ⇒ x1 = 0 lub x2 = 1 (dla I ćwiartki) Wzór na objętość V = π∫[a,b] y²dx Objętość bryły z obrotu funkcji y = √x

	x2		12		02
V1 = π∫[1,0]xdx = π*(		[1,0]) = π(		−		) = π/2
	2		2		2

	x5		15		05
V2 = π∫[1,0]x4dx = π*(		[1,0]) = π(		−		) = π/5
	5		5		5

V = V1 − V2 = π/2 − π/5 = 3*π/10

AS: Jak zwykle chochlik rozrabia − winno być (granice całkowania) V1 = π∫[0,1]xdx =... i dalej tak samo.

AS: Jeszcze jedna poprawka Szukam punktu wspólnego dla obu krzywych x² = √x ⇒ x⁴ = x ⇔x*(x³ − 1) = 0 ⇒ x1 = 0 , x2 = 1

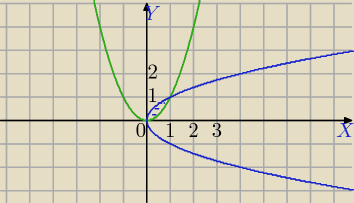
Mila: y=x² i x=y². x=(x²)² x−x⁴=0 x(1−x³)=0 x=0 lub x=1 Dalej wg wskazówek AS−a.