Trygonometria Nie umiem: Czy takie dzialanie jest dozwolone?

	2π		3π		6π
sin		* sin		= sin
	5		5		25

ICSP: nie

Nienor: to smutne.

	2π		3π
sin		* sin		≈ 0,951 + 0,951 = 1,902 ≠ od sinusa jakiego kolwiek kąta.
	5		5

ICSP: zamienić mnożenie na dodawanie

Nienor: ojoj, 0,951*0,951=0,904401

	6π
sin		≈ 0,6845
	25

Godzio:

	2π		3π		6π		6π2
A dlaczego		*		=		, a nie		?
	5		5		25		25

Nienor: Godzio dobre pytanie, ale to dalej nie działa :

	6 π2
sin		≈ 0,6982
	25

Nie umiem:

Nie umiem: Jak wiec moge sie rozprawic z takim przykladem?

	π		2π		3π		4π		5π
sin		*sin		*sin		*sin		*sin		?
	5		5		5		5		5

Przy okazji, w ksiazce mam podany takowy sposob na zapamietanie wzorow redukcyjnych: "Zakladamy, ze alfa jest miara kata ostrego i sprawdzamy, jaki znak ma interesujace nas wyrazenie, zapisujemy go po prawej stronie znaku rownosci. Jezeli liczba poprzedzajaca −/+

	π
alfa jest nieparzysta wielokrotnoscia		, wowczas funkcja zmienia sie na kofunkcje, jesli
	2

nie, funkcja pozostaje bez zmiany." Czy tym sposobem moge sie rowniez posluzyc w powiedzmy, takim przykladzie?:

4π		0,(4)π
	=		<− czyli wielokrotnosc ta jest tu nieparzysta?
18		2

Basia:

	5π
sin		= sinπ = 0
	5

czy teraz iloczyn już łatwo policzyć ?

Nie umiem: Tak, bedzie wynosil 0, to jednak nie rozwiazuje calkowicie mojego problemu. Powiedzmy, ze mamy podobny przyklad, lecz bez ostatniego wyrazu... co wowczas robimy?

Nienor:

	5π
sin		=sinπ=0
	5

ICSP: zależy od przykładu.

Basia: nie zawsze da się to wtedy policzyć tu byłoby

	4π		π		π
sin		= sin(π−		) = sin
	5		5		5

	3π		2π		2π
sin		= sin(π−		) = sin
	5		5		5

iloczyn = (sin^π₅*sin^2π₅)² dalej można próbować opierając się na wzorze

	x+y		x−y
cosx − cosy = −2sin		sin
	2		2

ale nie wiadomo czy to coś da te kąty muszą być odpowiednio dobrane, żeby dało się policzyć

ICSP: albo po prostu rozwiązać równanie x⁵ = 1

Nie umiem: No to podam inny przyklad.

	4π		5π		6π
ctg		*ctg		*ctg		=?
	18		18		18

ICSP:

4π

5π

6π

4π

4π

π

ctg

* ctg

* ctg

= ctg

* tg

* ctg

= 1 *

18

18

18

18

18

3

	π		√3		√3
ctg		= 1 *		=
	3		3		3

Basia:

π		9π
	=
2		18

	5π		9π		4π		4π
ctg		= ctg(		−		) = tg
	18		18		18		18

tgx*ctgx = 1

	6π		π		√3
ctg		= ctg		=
	18		3		3

wystarczy ?

Nie umiem: Wystarczy, dziekuje, a teraz dalej. Czy to zrobilem poprawnie? 4*sin(−420)=4*sin(−360 − 60)=4*(−sin60)= −2√3 O ile dobrze rozumiem, w tym przypadku drugie ramie tego kata jest w czwartej cwiartce, przy czym przechodzi tez raz przez pozostale?

Basia: dobrze ważne jest tylko położenie końcowego ramienia kąta, ile razy, jak napisałeś, przechodzi przez pozostałe nie ma znaczenia można też było tak, na podstawie wzoru sin(−x) = −sinx : sin(−420) = −sin420 = −sin(360+60) = −sin60

Nie umiem: Dziekuje Basia. Raczej nie zamierzam sie uczyc wzorow redukcyjnych, chyba, ze okazalo by sie, ze jednak lepiej sie ich nauczyc. Jak dotad korzystalem z tego sposobu, ktory zaprezentowalem kilka postow wczesniej i musze powiedziec, ze sprawdza sie bardzo dobrze.

Basia: tak trzymaj bo to najlepszy sposób

Nie umiem: Jeszcze jedno pytanie, ktore czesciowo nawiazuje do tego wlasnie sposobu. Wezmy na przyklad wartosc sinπ. Jesli sie nie myle, to drugie ramie tego kata lezy na ujemnej osi OX, ale nalezy juz do trzeciej cwiartki ukladu, wiec po redukcji pod uwage bierzemy wartosc −sin0, minus dlatego, ze sin w trzeciej cwiartce przyjmuje wartosc ujemna, zgadza sie?

Nie umiem: Nikt nie wie?

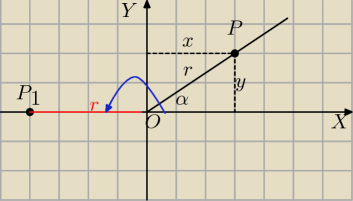
Mila: sinπ=0 cosπ=−1 To wynika z definicji funkcji w układzie współrzędnych |OP|=r

	y
sinα=
	r

P1(−r,0) − punkt na ramieniu kąta α=π

	0
sinπ=		=0
	r

	x		−r
cosπ=		=		=−1
	r		r

Nie umiem: Hmm, dziekuje, w sumie to nie do konca o to mi chodzilo, kiedy zadawalem pytanie, ale z drugiej strony przyblizylo mi to tez interpretacje funkcji trygonometrycznych kata 0 stopni, o ktora chcialem zapytac. Z kolei, czy punkt P1 to nie powinien byc raczej taki: (−x,0) ? Teraz jeszcze sprecyzuje troche bardziej moje pytanie nawiazujace do metody opisanej przeze mnie o godz. 17:27, dokladnie chodzi mi o czesc "sprawdzamy, jaki znak ma interesujace nas wyrazenie". Czy w takich przykladowych sytuacjach jest tak, jak to sobie wyobrazam? np. 1. cos5π, drugie ramie lezy na ujemnej osi OX, znak interesujacego nas wyrazenia to minus (patrzymy na trzecia cwiartke) 2. ctg2π, drugie ramie lezy na dodatniej osi OX, znak interesujacego nas wyrazenia to + (patrzymy na pierwsza cwiartke) 3. −ctg2π, drugie ramie kata lezy na dodatniej osi OX, znak interesujacego nas wyrazenia to minus (patrzymy na trzecia cwiartke) A pytanie brzmi mianowicie, czy w przypadku, kiedy drugie ramie kata lezy na ktorejs z osi, to czy w przypadku okreslania znaku interesujacego nas wyrazenia patrzymy, jaki znak ma poczatkowe wyrazenie w cwiartce, do ktorej zmierza (czyli bywa roznie w zaleznosci od tego,czy kat rysujemy zgodnie czy przeciwnie do ruchu wskazowek zegara)?

Nie umiem: Anyone?

Nienor: To nie jest jakiś sobie kąt, tylko kąt skierowany, więc nie można go sobie rysowac w drugą stronę

AS: Korzystam z tożsamości sinα*sinβ = 1/2*[cos(α − β) − cos(α + β)] W tym przypadku sin(3*Pi/5)*sin(2*Pi/5) = 1/2[cos(3*pi/5 − 2*Pi/5) − cos(3*Pi/5 + 2*Pi/5)] = 1/2*[cos(Pi/5) − cos(Pi)] = 1/2*[1/4*(1 + √5) − (−1)] = 1/8(5 + √5)